Hallo,
heute habe ich für euch ein kleines Problem zum Nachdenken.
Es geht um den selbstgebauten Planetariums-Projektor, siehe
http://www.astrotreff.de/topic.asp?TOPIC_ID=177112
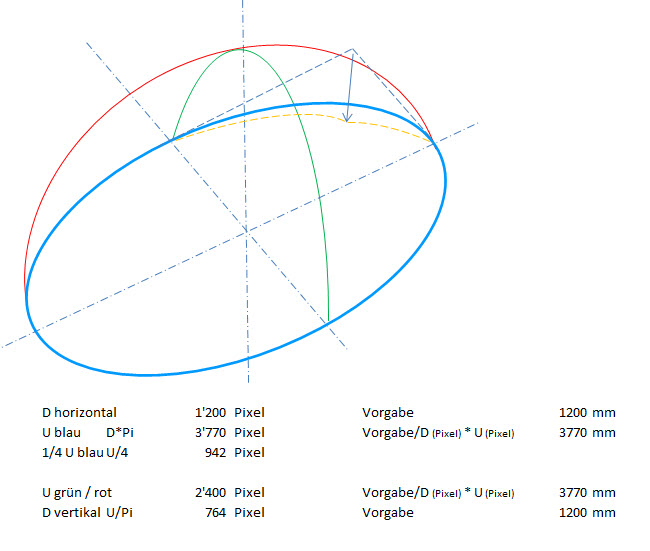
Der Projektor hat in vertikaler Richtung eine Auflösung von 1200 Pixeln. Das Fisheye-Objektiv bildet einen Kreis mit 1200 Pixeln Durchmesser in die Halbkugel ab.
Das Objektiv bildet in guter Näherung alle Abstände in radialer Richtung mit dem gleichem Maßstab ab. 1200 Pixel auf 180°, das ergibt also jeweils 66.7 Pixel für jeden 10° Abschnitt. Da man mit Stellarium das azimutale Gradnetz einblenden kann, kann man sich davon überzeugen dass die 10° Abstände entlang des Meridians alle gleich groß dargestellt werden.
In der Halbkugel ist die 360° lange Horizontlinie zweifellos genau doppelt so lang wie der 180° lange Meridian (von Süd über Zenit nach Nord). Demnach müsste die Horizontlinie eine Länge von 2400 Pixeln haben (weil der Meridian zweifellos 1200 Pixel lang ist).
Aber jetzt kommt der Widerspruch: Ein Kreis mit 1200 Pixeln Durchmesser hat einen Umfang von 1200*Pi=3770 Pixeln. Die Horizontlinie ist also 3770 Pixel lang.
Wo ist der Fehler in meiner Argumentation?
Ich kenne die Lösung schon, aber ich lasse euch auch mal nachdenken damit die Gehirne nicht einrosten.
Gruß
Michael
P.S. Die Lösung kommt morgen.