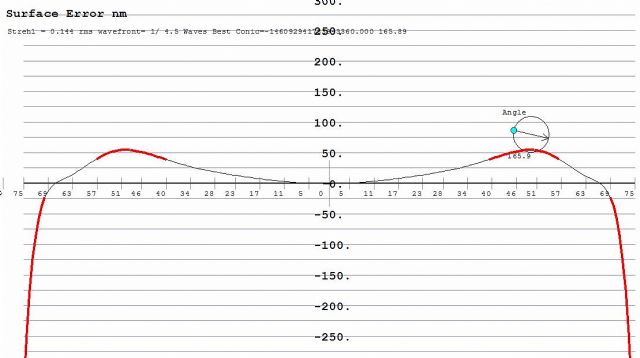
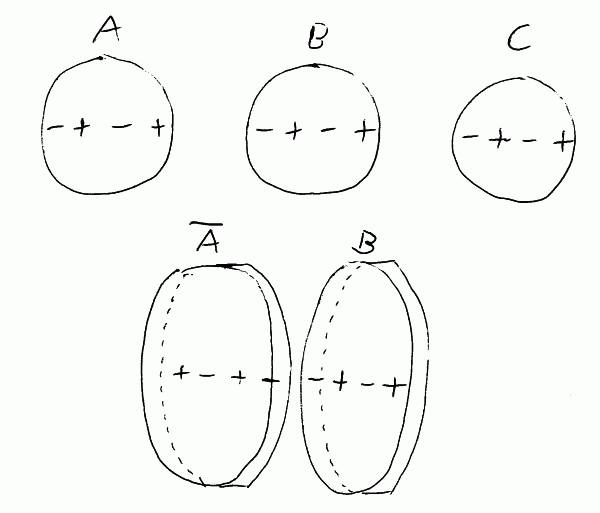
Angefangen hat das im April so: Drei Scheiben von Stathis mit 150 mm Durchmesser und 11 mm Dicke werden im 5-Minuten-Turnus mit Microgrit 15 abwechselnd gegeneinander geschliffen. Nach dem ersten Durchgang ist noch eine leichte Sattelform zu erkennen...
... aber nach der nächsten Runde geht der Kontakt bis zum Rand. Der Feinschliff runter zu Microgrit 1 ist am nächsten Tag beendet. Das Schöne am feinen Pulver: Nach nur 5 Minuten Politur sind die Scheiben schon so blank, dass sie aufeinandergelegt im gelben Natriumlicht deutliche Interferenzstreifen zeigen.
Dann geht der Tanz um die Oberfläche los und dauert fast drei Monate. Die Tochter fragt zwischendurch, ob außer komischen gelben Bildern auch mal wieder die Familie fotografiert wird - aber eines Tages kommt der Papa aus dem Keller mit diesem verklärten Blick, den sie schon von der Fertigstellung des Hauptspiegels kennt.
Und dann naht unweigerlich der Moment, vor dem mir lange gegraust hat: Aus einer der kostbaren Platten einen elliptischen Fangspiegel herauszubohren.
Damit die Platte beim Bohren nicht verkratzt oder ausbricht, wird auf jede Seite eine dünne Scheibe mit Pech aufgeklebt. Dazu werden auf die dünnen Scheiben jeweils Pechkrümel gelegt und diese im Backofen geschmolzen. Die ebenfalls erwärmte Planscheibe wird wie bei einem Burger dazwischen gelegt. Gegen eventuelle Luftblasen wird der Burger im Backofen zwischen 2 Holzbrettern und Schraubzwingen langsam gepresst. Das Bild mit dem Burger passt: auf allen Seiten quillt die Soße raus, deshalb unbedingt eine Serviette drunter legen. Dann alles langsam abkühlen lassen. Oben das Bild vor der Pech-Kleberei: Die Filzplättchen dienen zum Zentrieren, die Papierstreifen sind Abstandhalter, damit Glas nicht auf Glas reibt.
Dann kommt der Bohrer zum Einsatz: Ein passendes Dachrinnen-Rohr mit 85 mm lichter Weite aus Zink. Das erscheint mir runder als alles, was ich selbst aus Blech biegen könnte.
Der Glas-Burger wird unter einem Winkel von 35° eingegipst - der ist durch die Länge der Glasscheibe und die Größe der Gipskiste vorgegeben. Vier Rollen aus dem Baumarkt sorgen dafür, dass das Rohr genau an der richtigen Stelle bohrt.
Nachdem der Gips ausgehärtet ist, kommt dann das Fitness-Studio: der Motor bin ich - es wird abwechselnd an den beiden Seilenden gezogen! Das erinnert irgendwie an die Armarbeit auf einem Langlauf-Trainer. Zunächst habe ich keine Ahnung, wie lange das dauern wird, aber mit 180er Karboschlamm, der ab und zu erneuert wird, ist der Workout nach weniger als drei Stunden beendet.
Und dann noch ein spannender Moment: Ob sich der Spiegel durch das Ausbohren verzogen hat? Das könnte ja bei inneren Spannungen im Rohling passieren. Das vorerst letzte "gelbe Foto" hat aber diese Sorge behoben: Die Interferenzstreifen sind noch genau so gerade wie zuvor!
Jetzt noch mit dem Schleifstein unter Wasser eine Fase ziehen und dann nichts wie ab zum Verspiegeln.
Da ich den zugehörigen 18-Zöller bisher nur gemesen habe...
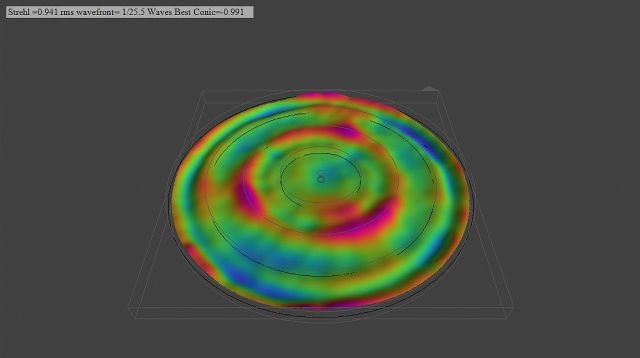
... möchte ich den endlich am Stern testen, bevor er ebenfalls verspiegelt wird. Immerhin liegt der ja seit letztemm September und wartet auf sein First Light... Der passende Lowrider ist ja schon gebaut, aber das ist eine andere Geschichte.
Werde berichten, wie es weiter geht...
Gruß
Norbert