Das Röhrchen (Zweilinser in F/9) besitze ich nun schon seit fast einem Jahr und habe es auch relativ häufig benutzt. Dabei sind mir niemals Farbfehler aufgefallen. Bisher haben ich auch jeden Farbsehtest problemlos bestanden. Also Farblindheit ist bei mir nicht. Nachdem ich aber vor 10 Tagen eine einschlägige Diskussion in astronomie.de intesiv verfolgt und auch selbt daran teilgenommen habe kommen mir doch potentielle Farbränder des Refraktors in den Sinn, siehe:
http://forum.astronomie.de/php…ein_ED_102_714#Post590875
Kurz und gut, ich wollte es halt genauer wissen. Wenn man messen kann ist das dabei recht vorteilhaft. Es ist zwar irgendwie blödsinnig einen Fehler vermessen zu wollen den man gar nicht sieht, aber Spaß muss auch sein. Außerdem hab ich dem Kollegen einen ensprechenden Bericht versprochen. Den kann ich aber wegen der für mich unzumutbaren Bilddokumentation in astronomie.de nur hier bringen.
Also erinnerte ich mich an meine ersten Versuche mit dem Bath- Interferometer mit verschiedenfarbigen LEDs anstatt mit Lasern vor mehr als 4 Jahren. Siehe meinen Beitrag mit Bildern am des Ende der Diskussion:
http://www.astrotreff.de/topic.asp?ARCHIVE=true&TOPIC_ID=17200&SearchTerms=zufällige,Fehler
Für die Farbfehlervermessung am Refraktor ist es aber günstiger, wenn man das Interferometer mit Weißlicht betreibt und mittels Farbfilter Intererogramme bei diskreten Wellenlängen produziert. In meiner „Schatztruhe“ fand ich zum Glück auch einige passende Inteferenzfilter mit den Wellenlängen:
475, 546, 589 und 675 nm.
Das reicht also von sattblau bis tiefrot.
Hier erst mal das nicht maßstabgerechte Schema meines auf Weißlicht umgetrimmten Bath- Interferometers:
<b>Bild 1</b>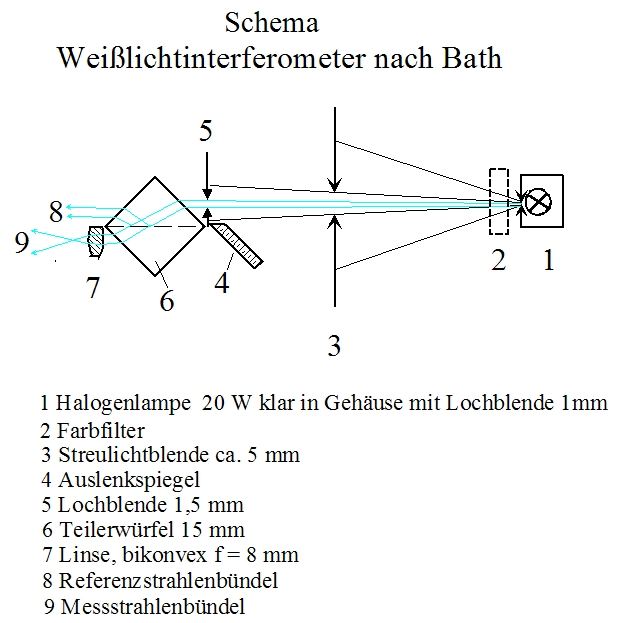
Der Abstand zwischen der Blende 5 und der Lochblende im Gehäuse beträgt ca. 300 mm
Als potentiellen Ersatz für die Halogenlampe hab ich mir schon einige weiße Hochleistungs- LEDs besorgt, aber noch nicht getestet. Weitere Fragen dazu werde ich gerne in der Diskussion beantworten.
Refraktoren interferometriert man üblicherweise in Autokollimstion (kurz AC) . Dabei stellt man hinten auf der Okularseite das Interferometer hin und dicht vor dem Objektiv einen Planspiegel.
Ein „Weißlichtinterferogramm“ ohne Filter sieht ungefähr so aus:
<b>Bild 2</b>
Vom Interferogramm her müsste ist diese Art von Interferometer eigentlich Buntlichtinterferometer heißen. Das Bild könnte man per Bildbearbeitung in die Grundfarben zerlegen und die Interferogramme auswerten. Die Sache hat aber zwei Haken:
1.Man ist an die drei Grunfarben des Kamera- Farbchips gebunden, deren effektive Maxima nicht so präzise angegeben werden können wie bei Interferenzfiltern.
2.Der Blaulichtanteil ist bei Verwendung von Halogenlampen relativ gering. Dazu kommt noch, dass er das je nach Qualität des Teilerwürfels nochmals in relativ zum übrigen Spektrum gemindert wird. Das kann dazu führen, dass ein zwar blau aussehendes Intererogramm in Wirklichkeit der Wellenlänge für blaugrün entsüpricht. Kurz gesagt, die Kombination aus Bath- Weißlicht Interferometer – Farbchip der Kamera und Lichtquelle ist für Vergleiche andernorts schwierig zu reproduzieren. Nach einschlägigen Versuchen hab mich deshalb doch zur Messung mit den klar definierten Interfernzfiltern entschlossen. Den chronischen Blaulichtmangel kann man hier nämlich durch längere Belichtungszeiten kompensieren, ohne das andere Farben stören können.
Dagegen scheint die bildtechnische Farbtrennung in Verbindung mit einen AC- Ronchitest recht brauchbar zu sein. Dabei entfällt nämlich die undefinierte Unterdrückung des Baulichtanteils durch das Interferometer. Einen derartigen Versuch hat Tommy Navratil im oben zitierten Astronomie.de Thread zur Diskussion gestellt.
Zurück zu meiner interferometrischen Vermessung:
Wie zeigen sich nun die typischen Farbfehler im Interferogramm? Als typisch meine ich hier
1.den wohl allgemein bekannten Farlängsfehler. D. H nicht alle Farben treffen sich in ein und demselben Brennpunkt.
2.Der sog. Gaußfehler auch farbabhängiger Öffnungfehler genannt. D. h. ein für grün ideal korrigierter Refraktor hat üblicherweise für blaues Licht eine sphärische Überkorrektur und für rot dagegen Unterkorrektur.
So könnte das ungefähr aussehen:
<b>Bild 3</b>
Das grüne I- Gramm gilt für einen perfekten Refraktor, der bei grün perfekt im Interferometer fokussiert ist (Die für die Streifenerzeugzung mimialen seitlichen Versetzung des Strahlenbündels kann man mit gutem Gewissen vernachlässigen). das rote sowie das blaue I-Gramm zeigen dem Fachmann, dass hier jeweils farbabhängige sphärische Aberration und Farblängsfehler präsent sind.
Wie kommt man nun an die eigenttliche Info, wie viel Farblängsfehler bzw. sphärische Aberration sind es denn und welche Wirkung hat auf die Abbhildungsqualität? Das geht ganz einfach. Man kann obige Interferogramm durch Berechnung aus frei wählberaren Parametern synthetisieren. Es bekanntlich genau so gut möglich echte Interferogramme zu analysieren und z. B. die hier interssanten Parameter Defokus und farbabhängige sphärische Aberration zu ermitteln. Dazu „verfüttert“ man die echten Interfeogramme an eine geeignete Auswertesoftware. Die sagt einem nach den Klicks auf die richtigen Buttons alles wissenswerte. Dazu bracht man neben Interferometer, Filtern und Planspiegel eigentlich nichts mehr.
Hier erst mal die zur Auswertung genutzen Interferogramme (aus Platzgründen auf 1/3 ihrer nat. Größe reduziert):
<b>Bild 4</b>
<b>Bild 5</b>
<b>Bild 6</b>
Warum denn gleich so viele? Weil ich 4 Wellenlängen gewählt habe. Um herauszufinden ob die Messung überghaupt etwas taugt muss man sie öfters wiedeholen. Außerdem ist es recht interessant zu erfahren, ob vielleicht die Steifenanzahl und Lage der Streifen einen merklichen Einfluss auf das Prüfergebnis haben.
Also, vor Beginn der Messserie wurde das Interferometer ohne Farbfilter so eingestellt dass man ungefähr ein Interferogramm wie Bild 2 sehen konnte. Danach wurde ohne irgendwelche Verstellungen am Interferometer nacheinasnmder die Farbfilter eingesetzt und die farbigen Interferogramme zwechs Auswertung fotografiert. Das Ganze wurde 3x wiederholt mit etwas anderer Streifeneinstellung pro Serie. Dabei muss man pingelig darauf achten, dass das Interferometer nicht ich nicht ein wenig angeschubst wird.
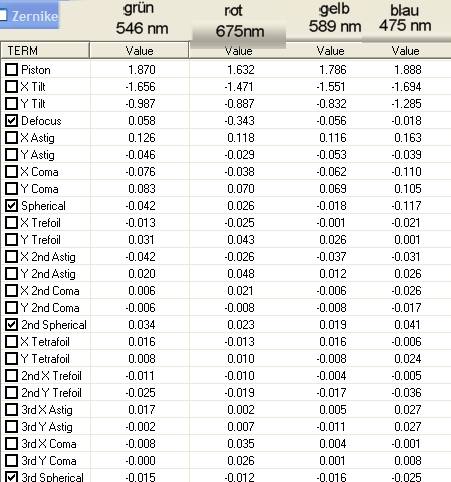
Hier sind wir schon bei der Ergebnistabelle:
<b>Bild 7</b>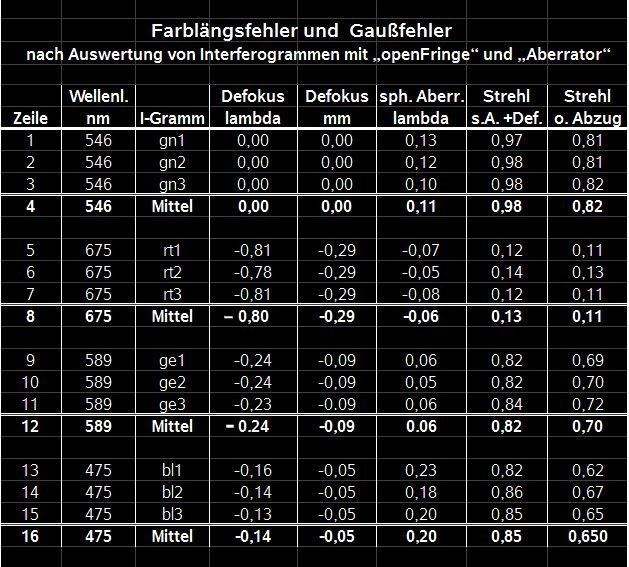
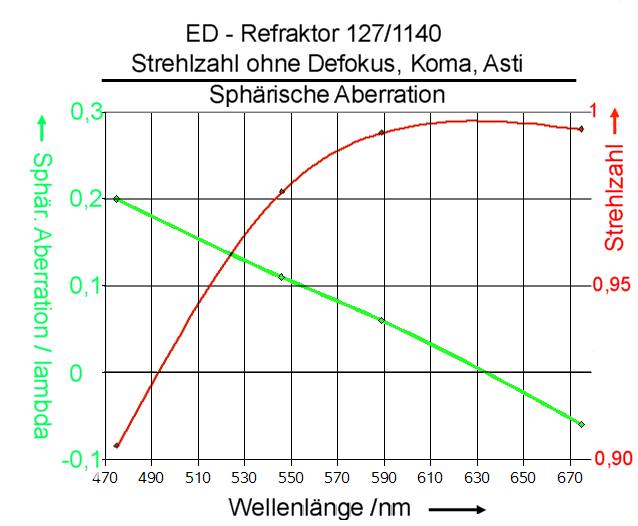
Schauen wir uns zunächst die Ergebnisse in den fett gedruckten Zeilen 4, 8, 16 und 16 an. Das sind die zu den einzelnen Wellenlängen gehörenden Mittelwerte. Die Wellenlänge 546 (grün) wurde als Bezug gewählt und demnach der Wert für Defokus = 0 gesetzt, indem man den für grün gemessenen Wert für Defokus abgezogen hat. Damit die Defokuswerte in für die anderen Wellenlängen dann noch richtig bleiben wurden diese ebenfalls um den für grün gemessenen Wert vermindert.
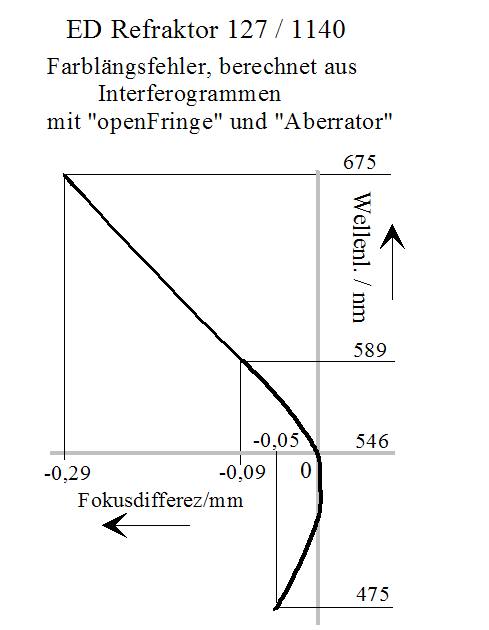
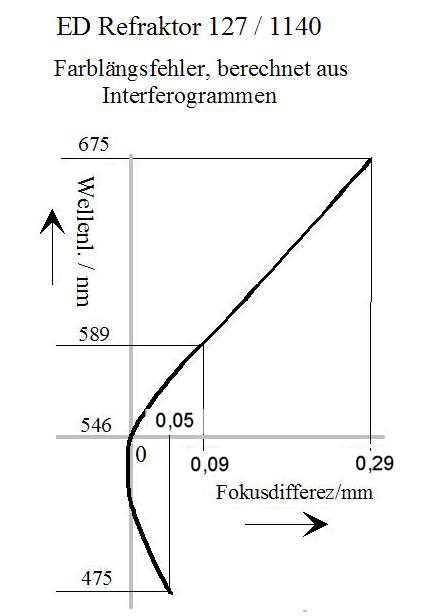
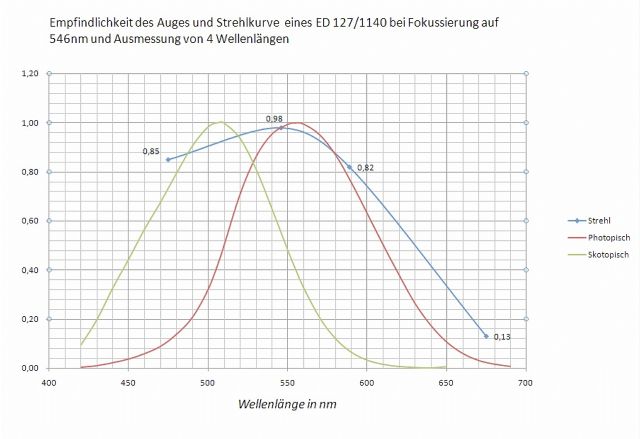
Das Auswerteprogramm „openFringe“ liefert über die Option „Profile“ die Defokuswerte im Wellenlängenmaß als Deformation derWellenfront. Dazu wird ausschließlich der Parameter „Defokus“ aktiviert. Die Defokussierung für 675 nm ist demnach mit 0,29 mm am größten. Für blau = 475 nm beträgt sie dagegen nur 0,05 mm. Danach wundert es mich auch nicht mehr warum der Refraktor keine Blausäume um helle Sterne produziert. Bei 675 nm ist das Auge vergleichsweise sehr unempfindlich, so dass der bei Fokussierung auf grün tatsächlich vorhandene Rotsaum nicht mehr wahrgenommen wird.
Die Umrechnung von Defokus in lamba auf mm hab ich dem Auswertewprogramm „Aberrator“ anvertraut. Man kann natürlich anzweifeln, ob die Ergebnisse richtig sind. Das lässt sich durch genau definierte mechanische Defokussierung des Interferometers (Verschiebung in Richtung der opt. Achse) und anschließender Auswertung wie oben überprüfen. Nach einer ersten Stichprobe kann ich sagen, dass man keinesfalls total daneben liegt. Eine spezielle Messerie dazu werde ich aber noch durchführen. Derartigen Tests muss man aber nicht für jedes einzelne Prüfobjekt durchziehen.
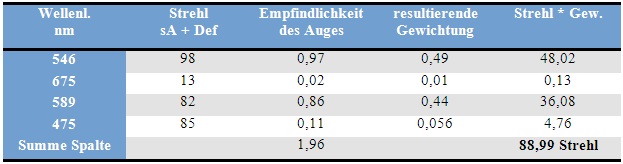
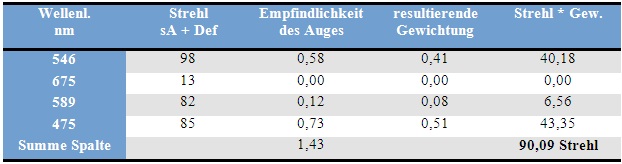
Mit der Option „Enable Spherial Only“ findet man ausschießlich die Werte für die sphärische Aberration. Nach Aktivierung dieses Parameters und anschließend von Defokus findet man die zugehörige Strehlzahl. Diese wäre also ein Maß für die optische Qualität bei den gemessenen Wellenlängen unter Einschluß von Farblängsfehler und wellenlängenabhängiger sphärischer Aberration (Gaußfehler) . Danach ist geht die Strehlzahl für rot total in den Keller. Für blau und gelb fällt sie im Vergleich zu grün signifikant ab. Wenn man will kann man das auch durch die entsprechende Aktivierung der Parameter als Strehl nur defokussierungsabhängig bzw. nur Gaußfehler auseinanderpflücken. Nur in der Praxis wirken immer beide Fehler!
Der Vollständigkeit halber sind auch noch die Strehlzahl ohne Abzug irgendwelcher Parameter aufgeführt. Sso wird die nahezu perfekte Strehlzahl 0,98 für Grün durch weitere Fehler ( hier Koma und Asti) auf 0,82 heruntergezogen. Eine sorgfältige Kollimation des Objektivs ist daher durchaus lohnenswert. Eine Neuvermessung des für mich nicht erkennbaren Farbfehlers werde ich mir aber schenken.
Wie man aus den Einzelwerten erhkennen kann sind die Streuungen erfreulich gering. Zur klassischen Fehlerdiskussion des Auswerteverfahrens müsste man aber noch etliche Wiederholungen mehr machen.
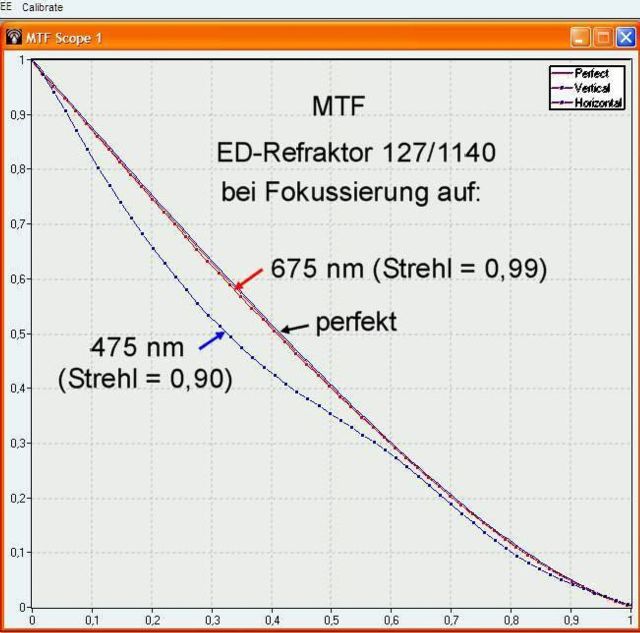
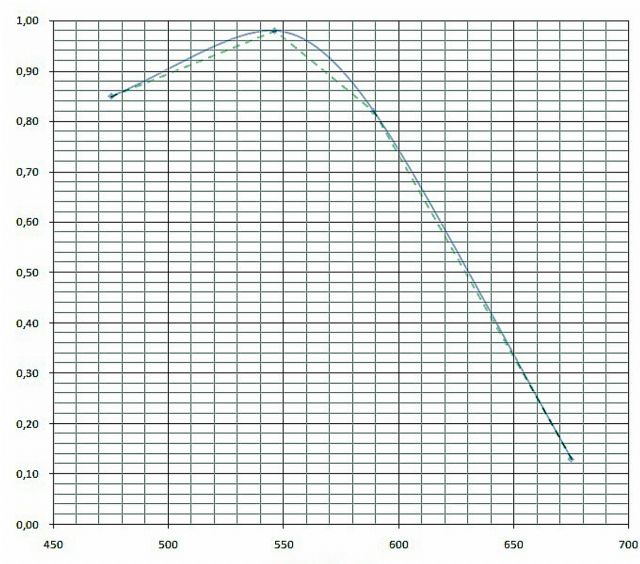
Noch wichtiger als die Strehhlzahl erscheint mir die Minderung der Kontrastübertragung (MTF- Funktion) als Folge von Defokus- und Gaussfehler. Solange man es mit echt hohen Strehlzahlen von 0,90 oder besser zu tun hat kann man sich die Darstellung der MTF zwar schenken, weil diese dann ebenfalls nahezu perfekt aussieht. Aber bei Strehl 0,82 z. B. wird die MTF doch hoch interesssant. Dummerweise unterdückt „openFringe“ grundsätzlich Defokus bei der Darstellung der MTF. Es tut so als sei das Teleskop immer bestens fokussiert. Hier kann wieder „Aberrator“ weiterhelfen (oder eigene Rechenkunst) . Man kann die Werte wie Defokus und sphärische Aberration aus „openFringe“ übernehmen und zusammen mit dem Öffnungsdurchmesser und Öffnungsverhältnis in „Aberrator“ eingeben. Danach ergeben sich diese Kurven:
<b>Bild 8</b>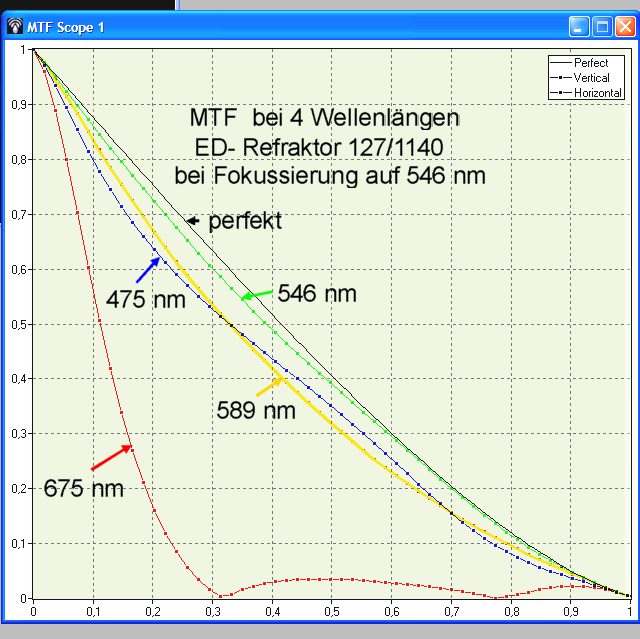
Für grün wäre der Refraktor nahezu perfekt, vorausgesetzt man kann Asti und Koma ausbügeln. Bei gelb und blau ist die Kontratüberagung eher schlechter als bei einem Spiegelteleskop mit mittelprächtiger Obstrukion und rot kann man ganz vergessen.
Sehr interessant könnte die demonstrierte Auswertemethode für die Beurteilung von f/7 oder gar f/6 „Superapos“ sein. Da findet man z. B. solche mit extrem geringen Farblängs- aber dafür mit um so dickeren Gaußfehlern...
<b>Fortsetzung 28.04.09 s. auch Seite 5</b>
Gruß Kurt