Hallo Kalle.
<blockquote id="quote"><font size="1" face="Verdana, Arial, Helvetica" id="quote">Zitat:<hr height="1" noshade id="quote">die niedrigeren Dichten zeigen dafür aber größere Strukturen<hr height="1" noshade id="quote"></blockquote id="quote"></font id="quote">
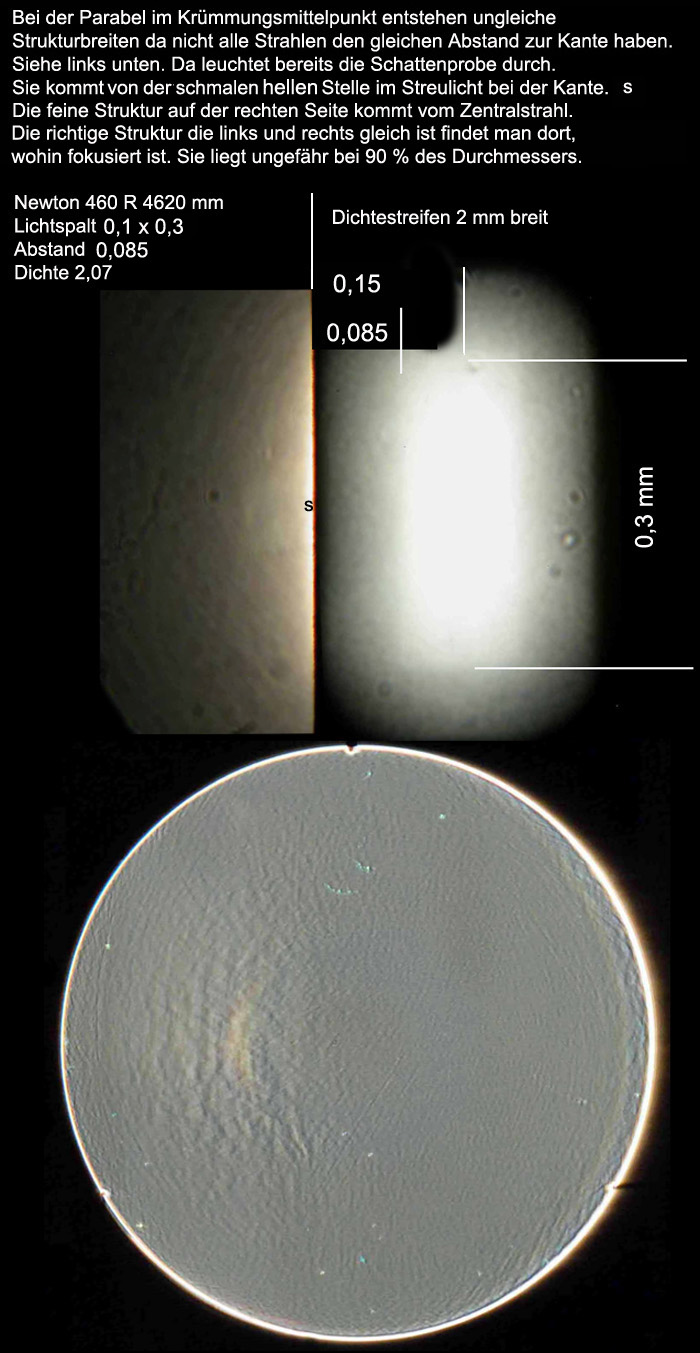
Das täuscht ein wenig. Siehe bei Dichte 4,5 da ist es ebenso.
Das hängt viel mehr davon ab, wie gleich man den Abstand trifft und das ist sehr Schwierig ihn immer gleich zu treffen.
Dazu noch ein Bild aus dem Krümmungsmittelpunkt das diese Abweichung stak zeigt.
In Autokollimation ist es leichter, aber das nützt unseren Teilnehmern wenig, da die meisten aus dem Krümmungsmittelpunkt
messen müssen. Bemühe mich auch deshalb vermehrt solche Beispiele zu bringen.
Bild 3
>> Horia.
Diese Bilder kann ich dir per E-Mail schicken.
Viele Grüße
Alois

