Beiträge von Specht im Thema „Iterationsgrafiken für Kepler-Lösungen“

Hallo Kalle!

Nö, es ging hier eigentlich nicht um C64-Historie. Obwohl ein C64-Thema mal was Schönes für´s OT-Forum wäre. (Würde vielleicht sogar den Katzenthread hinter sich lassen... [:D]) Es war halt der einzige Rechner, der zu jener Zeit auch komplexere Aufgaben lösen konnte. Wir verwendeten ihn sogar noch 1990 an der Uni als Protokollrechner (in der tragbaren SX64-Version).

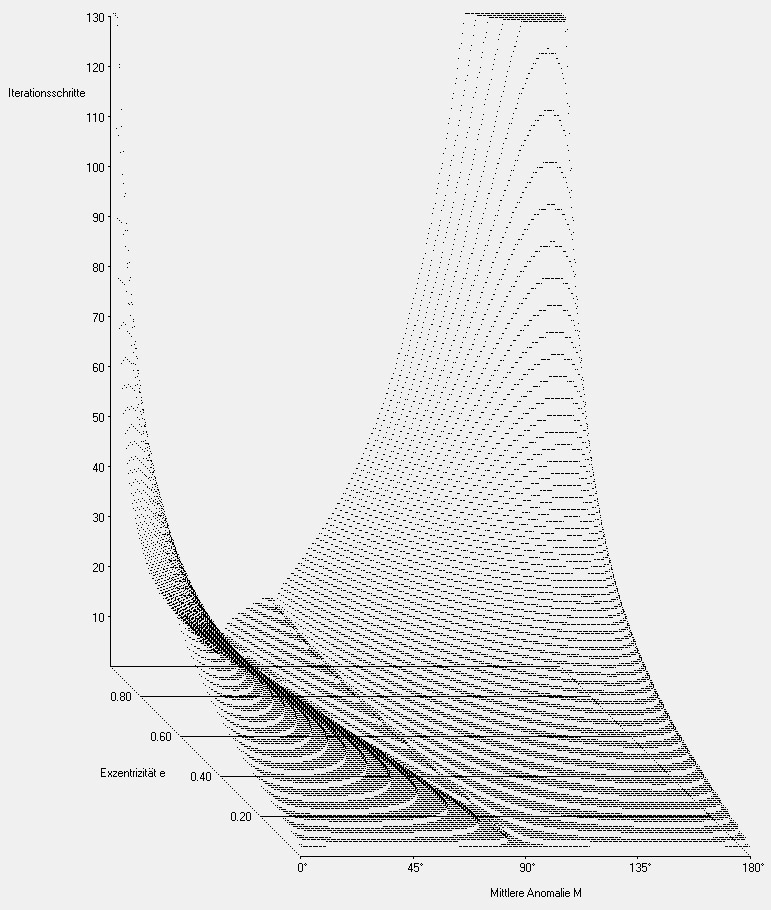
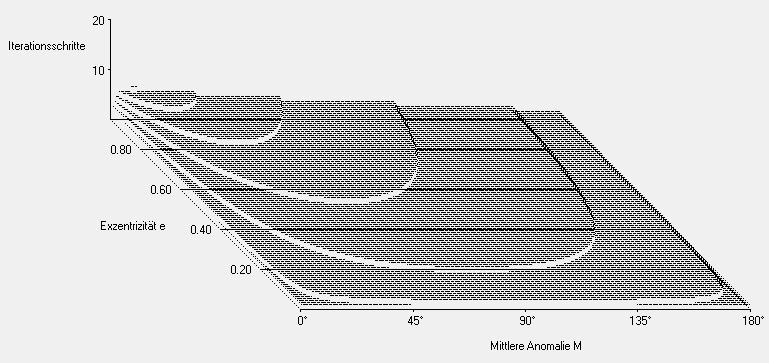
Neben den von mir oben gezeigten Methoden existieren wohl um die 100 andere Lösungsmethoden für die Kepler-Gleichung. Bei Stellen wie e>0.98 und M<10° verhalten sich manche extrem seltsam. Beispielsweise wird das Konvergenzverhalten von Methode II dort sehr instabil und spielt bei noch höheren Exzentrizitäten komplett verrückt.

In der astronomischen Praxis spielt das aber keine Rolle. Methode II verwende ich bis heute als Funktion kepler(m,ex) in meinen Programmen. Das alte, oben erwähnte Planetariumprogramm habe ich über so ziemlich alle Computer- und Betriebssysteme weiterentwickelt. Screenshots verwende ich dann gerne mal hier als Karte.

Sharp PC-1401 - ja, da schlägt doch mein Retro-Herz gleich schneller! Den konnte ich mir damals noch nicht leisten. Vor Jahren ergatterte ich mal auf einem Flohmarkt das Nachfolgemodell PC-1450. Da konnte man die RAM-Karten dann noch auswechseln. Neuwertig für ganze 10 Euro (den konnte ich mir dann leisten... [;)]). Ich arbeite neben dem schon oben erwähnten Casio FX-730P noch heute gern mit diesen Dingern.

Was mich hin und wieder dazu treibt, ein Thema über berechnende Astronomie zu öffnen, ist die Wahrnehmung, dass so mancher die fertigen Programme oder Apps langweilig findet. Viele möchten mal gern selbst z.B. eine Jupiter-Ephemeride berechnen. Endstation ist leider zu oft die Kepler-Gleichung...

salü, volker.

Hallo!

Nach einer Bitte zu den einzelnen schrittweisen Näherungen für E für das Beispiel (M=20°, e=0.3) habe ich diese mit einem alten Casio FX-730P einmal (übergenau) berechnet:

Methode I (Startwert 20°, siehe oben):

25.87889322° 28.09467924°
27.50237315° 28.09468976°
27.93750552° 28.09469254°
28.05306314° 28.09469328°
28.08367387° 28.09469347°
28.09177702° 28.09469352°
28.09392167° 28.09469354°
28.09448927°
28.09463948°

Methode II:

28.18682212°
28.09470780°
28.09469354°

In BASIC könnte man die Kepler-Gleichung z.B. mit einer Schleife lösen (hier im Gradmaß):

x=m
do
<font color="limegreen">ea = m + 180/pi * e * sin(x) (METHODE I)</font id="limegreen">
<font color="red">ea = x - (m - x + e * 180/pi * sin(x)) / (e * cos(x) - 1) (METHODE II)</font id="red">
if abs(x-ea) &lt; 0.00001 then exit do
x=ea
loop
exan=ea

m steht darin für die mittlere Anomalie, e für die Bahnexzentrizität, ea ergeben die jeweiligen Näherungswerte für die exzentrische Anomalie. Die gewünschte Genauigkeit legt man in der if-Anweisung fest, die Variable exan enthält danach den korrekten Wert für die exzentrische Anomalie. Aufpassen sollte man, in welcher Form die Programmiersprache das Argument des Sinus bzw. Cosinus erwartet. Wird Bogenmaß erwartet, muss man erst noch mit pi/180 multiplizieren.

salü, volker.

Hallo!

&rarr;Stick: Danke für dein Feedback per E-Mail - ich will hier kurz im Thema darauf eingehen, weil es vielleicht auch für andere interessant ist, die mit dem C64 Astronomiesoftware geschrieben haben (Thema C64, Assembler und Geschwindigkeit). Das Thema mit den Iterationsgrafiken stammt ja eigentlich aus dieser Zeit.

[specht]Große Planetariumprogramme ganz in 6510-Assembler zu schreiben, war mir wirklich zu umständlich, vor allem wegen der vielen Abstürze beim Austesten. Vor Simon´s Basic (SB) habe ich vor allem die Grafikroutinen damit gemacht. Als dann SB mit all seinen Möglichkeiten auf den Markt kam, war das für uns damals wirklich etwas wunderbares. Noch schneller ging es, als ich für verschiedene Funktionen neue, schnellere Routinen in Maschine schrieb, gerade für SQR (die C64-Routine dafür war erbärmlich) und ATN, die man mit SYS oder USR aufrufen konnte. Noch (erheblich) schneller ging es dann mit Näherungslösungen (x statt sin(x) bzw. 1-x&sup2;/2 statt cos(x) für kleines(!) x). Sternkoordinaten wie RA und DK wurden schon mit nur wenigen Dezimalen im Bogenmaß eingegeben, Spektraltyp und Leuchtkraftklasse mit nur einem Zeichen codiert. Der bedeutendste Geschwindigkeitssprung war allerdings die folgende Überlegung: die Höhe eines Sterns berechnet sich über den Arcussinus eines bestimmten Wertes. War dieser Wert negativ, so auch sein arcsin, d.h. er stand unter dem Horizont. So brauchte dieser nicht berechnet zu werden und erst recht nicht sein vor Winkelfunktionen wimmelnder Azimut. Das machte damals gleich einige Minuten Rechenzeit aus.[/specht]

Jüngere Amateure mögen jetzt schmunzeln, aber damals, die Zeit der ersten Heimcomputer wie VC20 oder C64, die hatte schon was. Der damalige, aus der Speichernot geborene Programmierstil spiegelt sich noch heute im Source Code mancher Programmierer wider.

salü, volker.

Hallo Wolfgang!<blockquote id="quote"><font size="1" face="Verdana, Arial, Helvetica" id="quote">Zitat:<hr height="1" noshade id="quote">Ich verstehe noch nicht so ganz die Botschaft, die du uns vermitteln willst. Dass bessere numerische Methoden schneller sind als Brute Force?<hr height="1" noshade id="quote"></blockquote id="quote"></font id="quote">Nein, natürlich nicht. Aber so mancher Sternfreund, der Interesse an der berechnenden Astronomie findet und selbst gerne z.B. Koordinaten von Planeten berechnen will, bleibt gerne an der Kepler-Gleichung hängen. Nicht jedem fällt das leicht, Kepler selbst arbeitete mit Logarithmentabellen und rief die Mathematiker seiner Zeit auf, Lösungsmethoden für seine Gleichung zu erarbeiten. Hin und wieder etwas Klassisches zu thematisieren, finde ich in einem Forum nicht uninteressant.

Heute hat wohl die klassische Ephemeridenrechnung mit Bahnelementen ihre Bedeutung zumindest bei den Planeten verloren. Professionelle Programme arbeiten hier meist mit den Termen der VSOP-Theorien.

Sobald ein Programm fertig ist, verliert es für mich beinahe jeden Reiz. Mein erstes "Planetarium-Programm" lief mit 300 Sternen auf einem C64 unter "Simon´s Basic". Eine Berechnung dauerte knapp drei Minuten. Der Kampf mit dem Speicherplatz und die Verbesserung der Rechengeschwindigkeit auch nur um Sekunden (z.B. durch eigene neue Maschinensprache-Routinen für SQR, SIN und COS) machte mir enormen Spaß. Mit jeder neuen Computergeneration wuchsen die Möglichkeiten, arithmetische Koprozessoren kamen. Trotzdem macht es Spaß, in der eigenen Software auch heute noch das Rad immer wieder selbst neu zu erfinden...

salü, volker.

Hallo!

Die Keplergleichung E = M + e * sin(E) (E: exzentrische Anomalie, M: mittlere Anomalie, e: Bahnexzentrizität) wird meist iterativ mit zwei verschiedenen Lösungsmethoden gelöst. Die einfachste Methode ist, zunächst M in die rechte Seite der Gleichung für E einzusetzen. Man erhält so eine erste Näherung für E. Diese Näherung setzt man dann wieder rechts für E ein und wiederholt das, bis eine angestrebte Genauigkeit erreicht ist. Im Gradmaß muss man noch den Faktor 180°/pi berücksichtigen:

E´ = M + e * (180°/pi) * sin(E) (Methode I)

Für M=20° und e=0.3 erhält man so mit dem Startwert E=20° nach 16 Iterationsschritten den korrekten Wert E = 28.09469354° (jetzt mal übergenau bis zur achten Nachkommastelle).

Die zweite Methode ist etwas komplizierter:

E´ = E - (M - E + e * (180°/pi) * sin(E)) / (e * cos(E) - 1) (Methode II)

Damit erhält man den korrekten Wert für E im obigen Beispiel bereits nach der dritten Iteration.

Interessant ist, die nötige Anzahl an Iterationsschritten einmal grafisch über einer (e,M)-Ebene darzustellen. Methode I erfordert bei höheren Exzentrizitäten sehr viele Schritte, besonders auch bei Werten für M nahe Null oder 180°. Zwischen M = 90° (pi/2) für e=0 und M &asymp; 32.7° (pi/2 - 1) für e=1 verläuft ein "Minimumgraben":

Die gleiche Grafik hier auch für Methode (II):

Sie ist damit für Programme wesentlich besser geeignet. Die Algorithmen zu den Grafiken entwickelte ich in den frühen Achtzigern noch auf einem C 64, der dann für eine ähnliche Darstellung ein paar Stunden brauchte... [;)]

salü, volker.