Hallo Rolf Rudi und Bernard
Vielen Dank für die Übersetzung und Anerkennung.
>>Bernard
<font color="yellow"> Ausgehend von dem, was ich davon verstanden habe, denke ich, dass ein Element der Antwort sich im Beitrag von Rainer vom 02 03 2014 um 1h21 befindet: </font id="yellow">
Ja Rainer hat dort die Lambda ¼ Schritte gut erklärt. Das könnte das von dir die als Delta (Phi) bzeichnete Funktion sein.
In diesen Fall aber als Differenz zwischen dem Lichtdämpfenden und dem Transparenten Teil, weil sich
nur der transparente Teil bewegt.
<font color="yellow"> "Bei den Bildern 13 und 14 steht "gemeinsam verschoben".
Dadurch ändert sich der Phasenunterschied zwischen dem direkten und gebeugten Licht nicht . Das Delta ist der Phasenunterschied zu einem Anfangswert . Eventuel gibt es noch einen Offsetwert ." </font id="yellow">
Hier ist vermutlich die Unklarheit der Bezeichnungen „Delta (Phi)“ und dem "zentralen Wert" von Phi“ zu finden.
Das Problem wird sein, weil ich Lambda ¼ Schritte gemacht habe und der optimale Kontrast auch eine Lambda ¼ Abhängigkeit hat.
Diese zwei Begriffe müssen getrennt behandelt werden.
Bei den Bildern 13 und 14 werden wohl Lambda ¼ Schritte gemacht aber es entsteht keine Phasendiffernz zwischen dem Lichtdämpfenden
und dem transparenten Teil.
Bei diesen Test wäre aber zu erwarten das sich im Lichtdämpfenden Teil die Kontrastoptimierende Lambda ¼ abhängige Wirkung zeigt.
Da hätte immer pro Lambda 1/2 Verschiebung eine Kontrastverstärkung und dann eine Kontrastabschwächung statt finden sollen.
Da dies nicht geschieht ist dies wohl eine nicht zutreffende Annahme. Wenn der Begriff (Phi)“ hier Zuständig ist dann steht auch er in Frage?
Damit hier eine klare Auseinanderhaltung entsteht, mache ich auf Wunsch von Horia und Michael noch eine Lambda 1/15 Animation.
Ja einen Offsetwert gibt es auch noch.
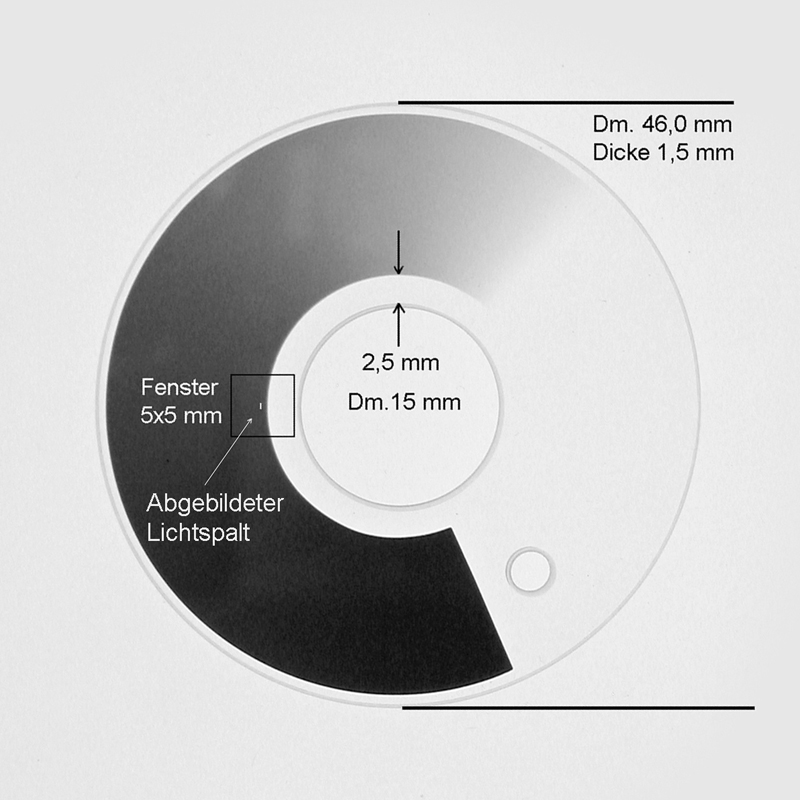
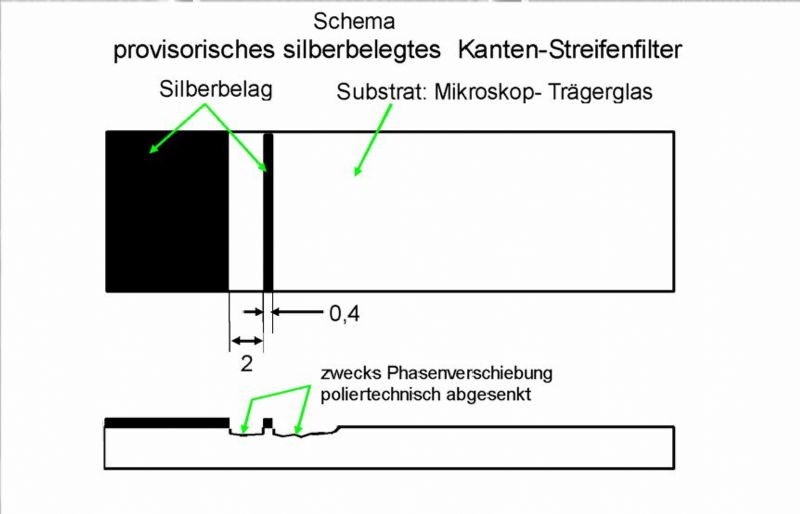
Das ist der Abstand der gedämpften Lichtbündelkante zur Kante des transparenten Teils. Für die grossen Ripple sind es 0,03 mm und für die
kleinen Ripple geht es bis zu dem Abstand von 0,20 mm. Dieser Abstand bleibt aber immer gleich und bestimmt nur die Breite der Ripple.
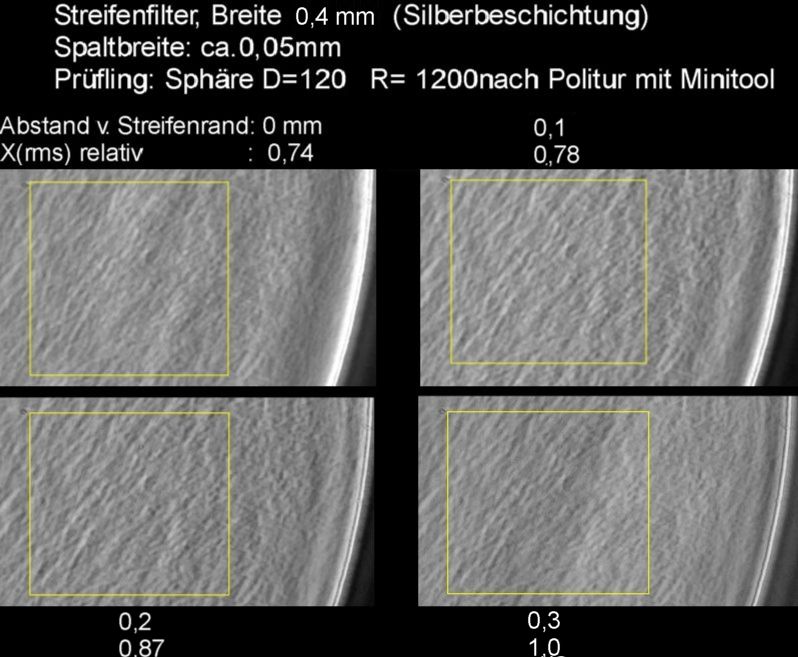
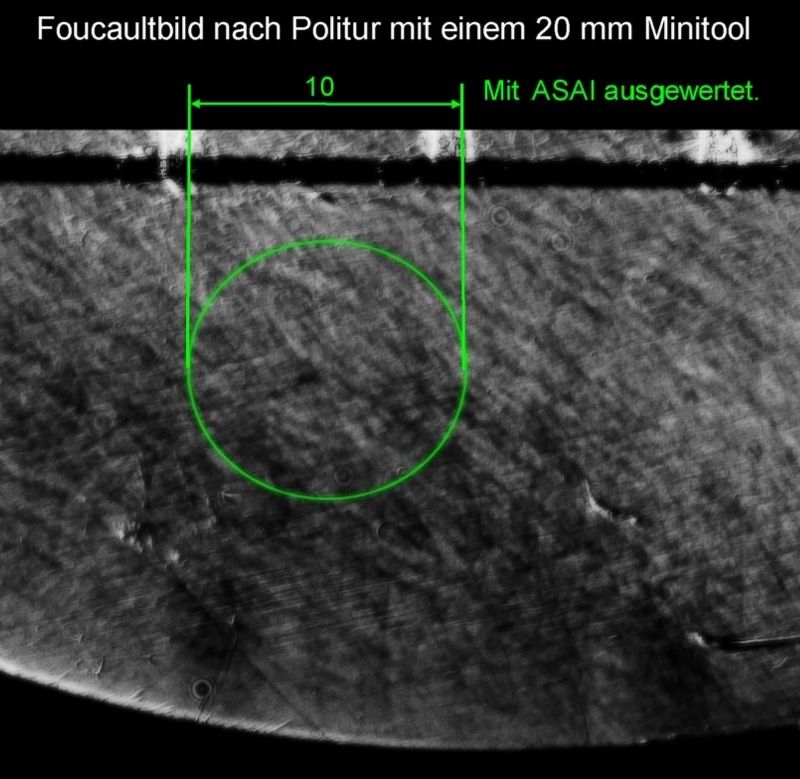
Das sieht im Fokus dann so aus. Die 0,3 mm ist die Grösse des gesendeten Lichtspalts, der aufgrund der sphärischen Aberration nicht scharf abgebildet ist.
Bild 26

Weiteres kann ich erst nach der neuen Animation erklären.
Viele Grüße
Alois