<b>1. Einleitung</b>
Eine ausführliche Beschreibung dieses Teleskops findet man unter
http://www.photoinfos.com/astronomie/Quantum-Q6-01.htm
Die nachfolgend beschriebenen Tests wurden an einem sehr gut erhaltenen Exemplar aus der Sammlung von Markus Ludes durchgeführt. Nach seiner Schätzung ist das Teleskop älter als 30 Jahre. Trotz dieses Alters konnte man augenscheinlich keine Defekte bezüglich Reflexionsgrad der Spiegelflächen zu erkennen.
Die Meniskus-Linse ist nicht vergütet. Der zentrale rückseitig verspiegelte Teil der Meniskuslinse bildet den Sekundärspiegel. Somit besteht die gesamte Optik aus drei sphärischen Flächen.
<b>2. Messgeräte und Zubehör</b>
Bath- Weißlichtinterferometer mit Halogenlampe
Twyman- Green Interferometer mit Diodenlaser 532 nm
Autokollimationsplanspiegel D = 300 mm
Interferenzfilter gemäß Tabelle
IR- Strahlungsthermometer
Tau-Raureif-Eliminator (TRE)
Taschenrechner
Kamera Nikon D5000 mit Objektiv AF Micro Nikkor 60mm 1 /2,8
<b>Bild 1</b>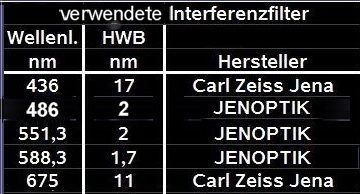
<b>3. Software</b>
OpenFringe Version 12.3 zur Auswertung der I-gramme
Bildbearbeitungsprogramm Photoline 32
<b>4. Aufgabenstellung</b>
<b>4.1 Wellenfrontanalyse zur Ermittlung der dominanten Restfehler, Strehlzahl und MTF für die Hauptwellenlänge grün (551 nm)</b>
Vor Beginn der Messung wurde das Teleskop zwei Tage lang im temperierten, zugfreien Prüfraum in der gebrauchsfertig eingerichteten Prüfvorrichtung gelagert. Die Raumtemperatur während dieser Zeit betrug 21,5°C mit max. Schwankung von ca. +/- 0,3°C
4.1.1 Genauigkeit der Messergebnisse
Zur Genauigkeit im messtechnischen Sinne findet man z.B. im
Brockhaus für Naturwissenschaft und Technik,
Zitat:
<i>„… Die G. wird bestimmt durch die Messunsicherheit und die Fehlergrenzen. Messunsicherheit lässt sich durch den Vertrauensbereich eines Mittelwertes aus mehreren Einzelmessungen charakterisieren…“</i>
(Zitat Ende)
Daraus folgt messerscharf: Wenn man mit der eigenen Prüfvorrichtung keine systematischen Versuche mit zur Messunsicherheit gemacht hat könnte man zur Genauigkeit der Messergebnisse nichts Zuverlässiges aussagen.
Es wäre nicht zwingend notwendig bei jedem neuen Prüfling den nachfolgend dokumentierten Aufwand mit zahlreichen Wiederholungen zu betreiben. So könnte ich die Daten zur Messunsicherheit aus früheren aber ähnlichen Versuchsserien mit gleichartigen Gerätschaften verwenden. Aber eine gelegentliche Auffrischung zur Frage nach der Genauigkeit kann ja nicht schaden. Also zur Sache:
Es wurde eine Serie von zehn I-grammen aufgenommen und ausgewertet.
<b>Bild 2</b>
<b>Bild 3</b> 
<b>Bild 4</b>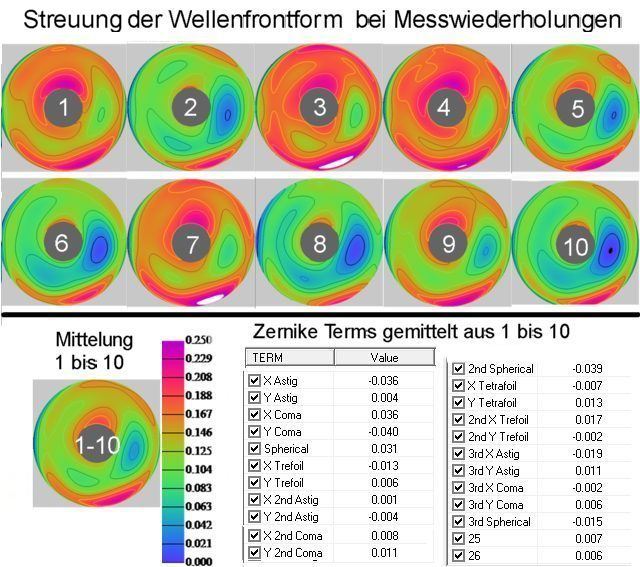
Nach Auswertung im „Zernike Based“ -Modus unter „openFringe“ erhält man die Daten zwecks Wellenfrontanalyse sowie zur Abschätzung der Genauigkeit.
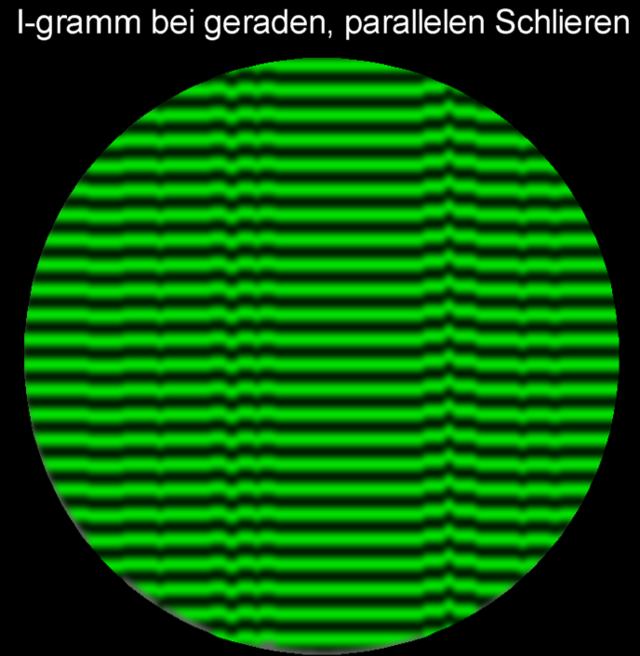
Man erkennt auf allen Bildern ähnliche Details:
a) Der äußerste Rand links ist abgesenkt
b) Oberhalb der Mitte ist ein Berg
c) Rechts von der Mitte ist eine Senke
d) Der Rand rechts unten ist angehoben.
Die einzelnen Wellenfrontbilder wurden zum besseren Vergleich mit einheitlicher Farbskalierung dargestellt. Die weißen Flecke in den Teilbildern 3 und 7 sind Bereiche in denen die Wellenfront geringfügig aus der gewählten Wellenlängenskala 0,000 bis 0,250. herausragt.
Nach der Tabelle der Zernike Terms sind die dominierenden Restfehler Asti, Koma sowie sphärische Aberration. Alle übrigen Restfehler (Trefoil, Tetrafoil etc.) zusammen verursachen nur 0,069 lambda Wellenfrontfehler als PtV- Wert bzw. 0,012 lambda RMS, entsprechend Strehlzahl = 0 ,994. D.h., die Summe der übrigen Restfehler ist verschwindend gering. Man kann deshalb mit gutem Gewissen auf deren individuelle Analyse verzichten. Sie wurden deshalb aber nicht aus der Ermittlung der Strehlzahl herausgenommen. Lohnend bleibt aber die Wellenfrontanalyse bezüglich Koma und Asti der Grundordnung sowie sphärische Aberration (Sphericals, alle 7 Ordnungen gemäß Openringe).
In der folgenden Tabelle sind die wichtigsten Ergebnisse aufgelistet.
<b>Bild 5</b>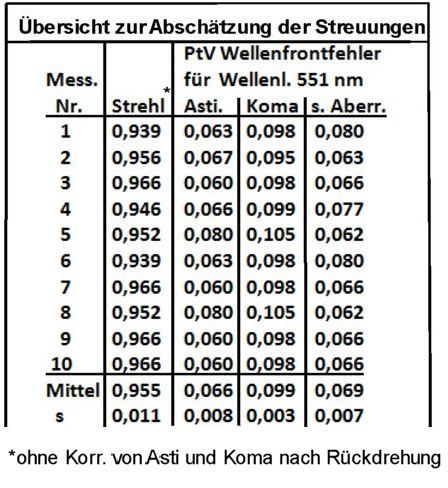
Die Mittelwerte wie z. B. 0,955 sowie die Schätzung der zugehörigen Standardabweichung s 0,010 wurden mit dem Taschenrechner berechnet.
Die PtV- Wellenfrontfehler wurden mit openfringe durch exklusive Aktivierung der entsprechenden Zernikes gewonnen. Hierzu als Beispiel für Mess. Nr. 1 Koma 0,092. Das folgende Bild zeigt die dazugehörigen Daten aus dem „Report“ .
<b>Bild 6</b>
Obige Mittel gemäß Tabelle <b>Bild 5</b> können durch Fehler der Prüfvorrichtung in Form von Koma und/oder Asti verfälscht sein. Dazu ein Zahlenbeispiel mit PtV- Werten. Angenommen sei:
Koma Versuchsaufbau= 0,1 lambda,
Koma Teleskop = 0,15 lambda.
Wie man erkennt kann Messwert im Bereich von 0,05 bis 0,25 schwanken, wenn das Teleskop in der Prüfstrecke um die opt. Achse gedreht wird.
<b>4.3 Quantifizierung der Restfehler</b>
<b>4.3.1 Asti</b>(gmatismus)
Dazu braucht man mindestens 1 weiteres I-gramm, aufgenommen bei axial um 90° gedrehter Position des Teleskops. Im Folgenden hab ich aber zur Reduzierung der Messunsicherheit jeweils drei I-gramme je Teleskopposition ausgewertet.
<b>Bild 7</b>
<b>Bild 8</b>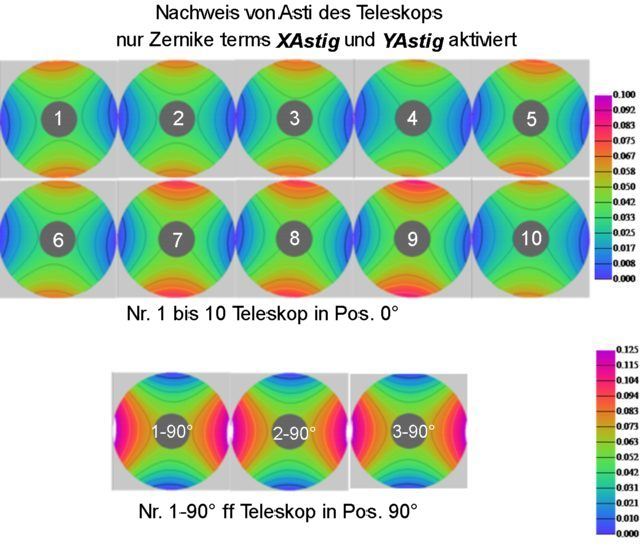
Der Asti hat sich offensichtlich nach Drehung des Teleskops um 90° in gleicher Weise gedreht. Das wird noch besser sichtbar wenn man die Teilbilder 1 bis 10 bzw. 1-90° ff. mittelt und nebeneinander stellt:
<b>Bild 9</b> 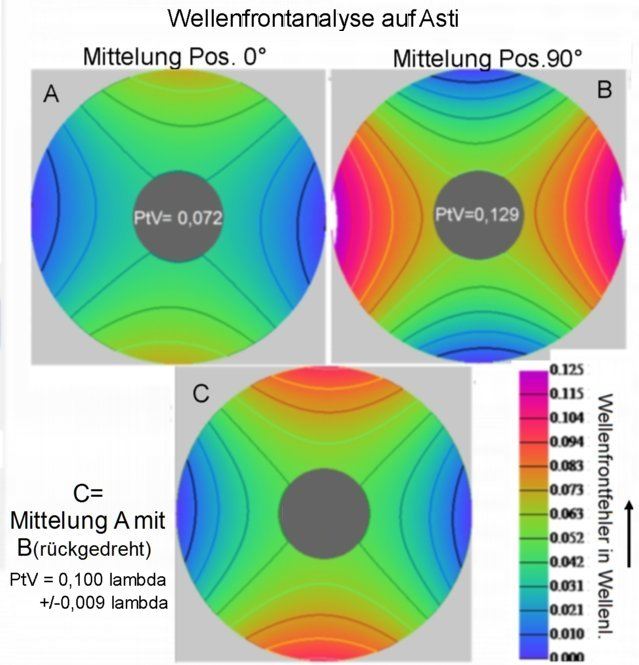
Die folgende Sterntestsimulation erlaubt eine Abschätzung ob denn die PtV 0.1 lambda Asti visuell erkannt werden können oder nicht.
<b>Bild 10</b>
Nach meinem Eindruck ist PtV 0,1 lambda Asti visuell noch nicht wahrnehmbar.
<b>4.3.2 Koma</b>
Hier wird das Teleskop um 180° gedreht und die danach erstellte Wellenfront mit der in Pos 0° verglichen. Dazu wurden analog wie bei Asti zusätzlich 3 I-gramme aufgenommen und ausgewertet.
<b>Bild 11</b>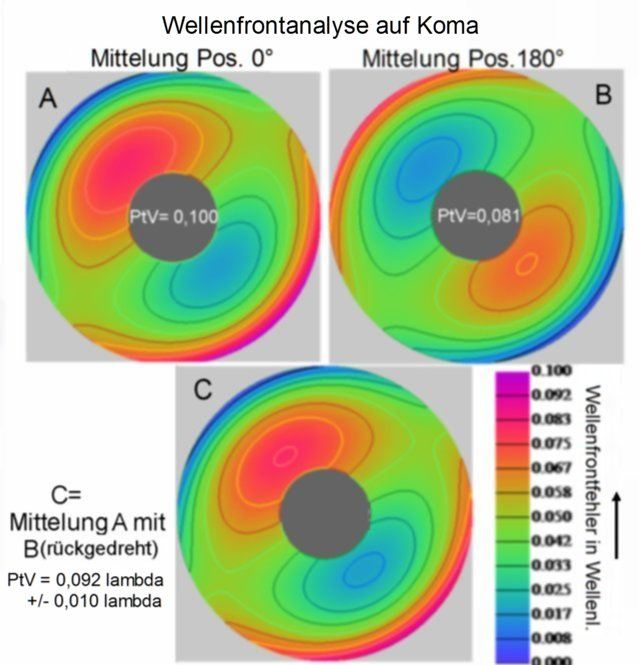
Koma ist damit ebenfalls zweifelsfrei messtechnisch nachgewiesen. Ob die gemessenen PtV = 0.092 lambda visuell bereits erkennbar sind halte ich aber für eher unwahrscheinlich. Nach meinem Empfinden würde ich das Teleskop spätestens ab PtV = 0,15 lambda als komatös bezeichnen. Ohne Drehung und Berücksichtigung des Prüfstandsfehlers wäre es reiner Zufall ob man das Teleskop als praktisch komafrei oder bereits störend komatös beurteilt. Davor schützt auch kein Sterntest auf dem Prüfstand, so lange man die 180°- Drehung des Teleskops nicht praktiziert.
<b>Bild 12</b>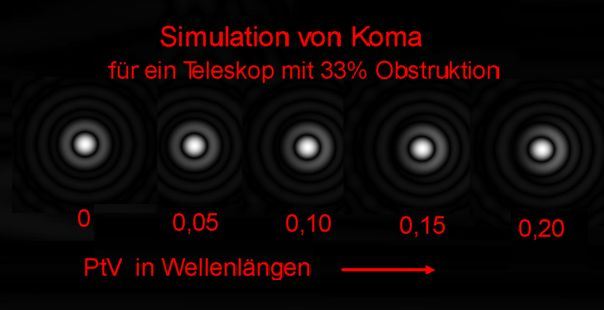
<b>4.3.3 Sphärische Aberration (sA</b>)
Dazu wurden die 3 I-gramme bei 551nm aus der weiter unten behandelten Farbmessserie ausgewertet.
<b>Bild 13</b>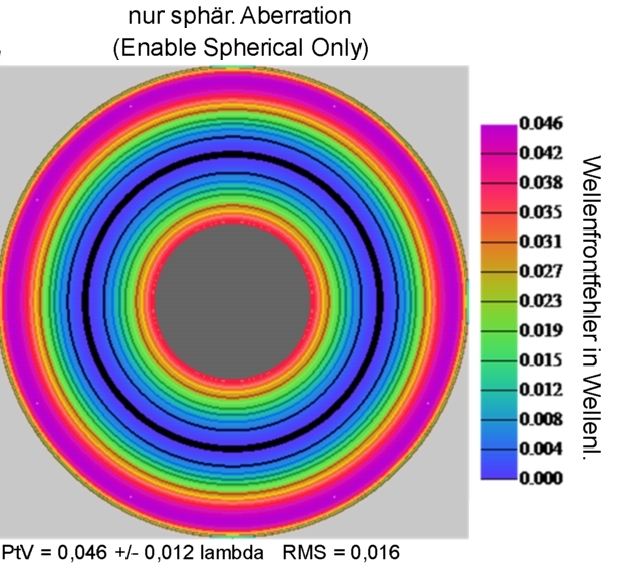
Da hier gemäß „openFringe“ alle 7 Ordnungen der sA aktiviert worden sind wäre die Angabe des PtV – Wertes allein nicht mehr eindeutig. Auf jeden Fall ist die gemessene sA aber sehr gering und damit visuell nicht auffällig.
<b>4.3.4 Strehlzahl bei 551 nm</b>
Kleinviech macht bekanntlich auch Mist. Daher bleiben auch die hier recht geringen Werte für Asti, Koma, sA und all die übrigen aktivierten Zernikes für die Strehlberechnung relevant. Alles andere führt nur zu unsinniger Schönung des Ergebnisses. Die Zernikes für Asti und Koma der Grundordnung wurden gemäß den Ergebnissen aus <b>4.3.2</b> bzw. <b>4.3.3</b> übernommen.
<b>Bild 14</b>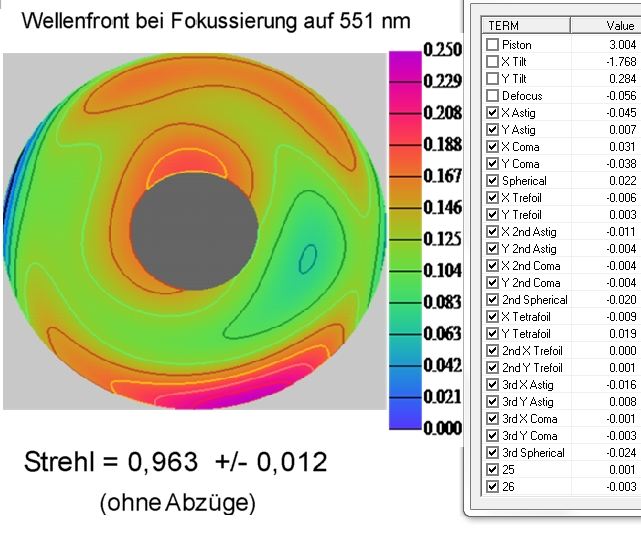
Die dritte Nachkommastelle sollte man nicht allzu ernst nehmen. Glaubhafter formuliert soll das heißen:
Die Strehlzahl bei Fokussierung auf grün liegt mit 95% Wahrscheinlichkeit im Bereich von 0.97 bis 0,95.
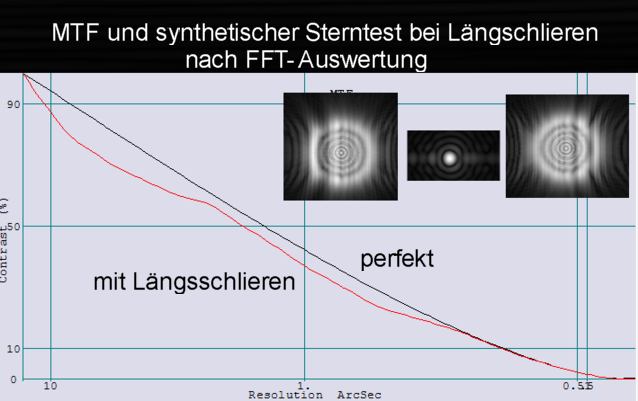
<b>4.3.5 Kontrastübertragungsfunktion MTF</b>
<b>Bild 15</b>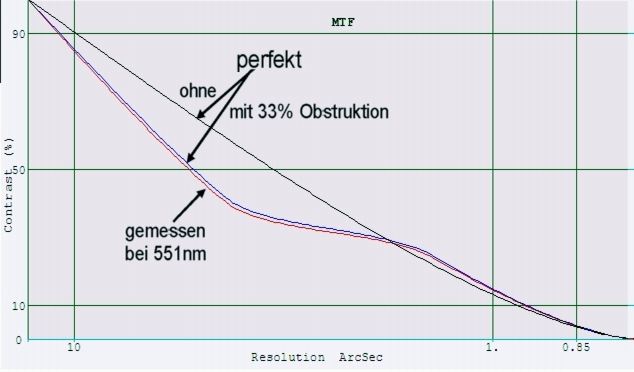
Zur Darstellung der realen Kurve wurden dieselben Zernike- Datensätze genutzt wie zur Ermittlung der Strehlzahl. Wie man sieht ist die Abweichung von der Idealkurve mit Obstruktion recht gering. Im mittleren Auflösungsbereich beträgt der Unterschied perfekt-real weniger als 4%. Die bisher betrachteten Restfehler bewirken demnach nur einen geringen Verlust. Der durch 33% Obstruktion verursachte Durchhänger der Kurve ist dagegen beträchtlich.
<b>4.3.6 Rauheit</b>
der opt. Oberflächen verursacht zwangsläufig Deformationen der Wellenfront. Das führt bei fokaler Abbildung von Sternen zur zusätzlichen Verdrängung von Licht aus dem zentralen Beugungsscheibchen in dessen Nachbarschaft. Das mindert definitionsgemäß die Strehlzahl. Ebenso wird dadurch die Kontrastübertragung reduziert.
Das Problem zur Erfassung der Rauheit bezüglich Strehlzahl und MTF ist messtechnischer Art. Die Rauheit wird mit der allgemein üblichen Interferometrie und auf Zernike- Basis arbeitender Auswertesoftware nicht erfasst.
<b>4.3.6.1 Makrorauheit</b>
Darunter sind hier Rauheitsstrukturen bis herab zur lateralen Ausdehnung von ca. 1 mm gemeint. Profi-Interferometer z.B. Zygo erfassen zumindest näherungsweise diesen Fehlerbereich der Wellenfront. Das zeigen z. B. die Messprotokolle von Orion Optics zu hochwertigen Teleskopspiegeln oder auch ähnliche praktiziert von den in Fachkreisen bekannten und geschätzten Herrn Rucks.
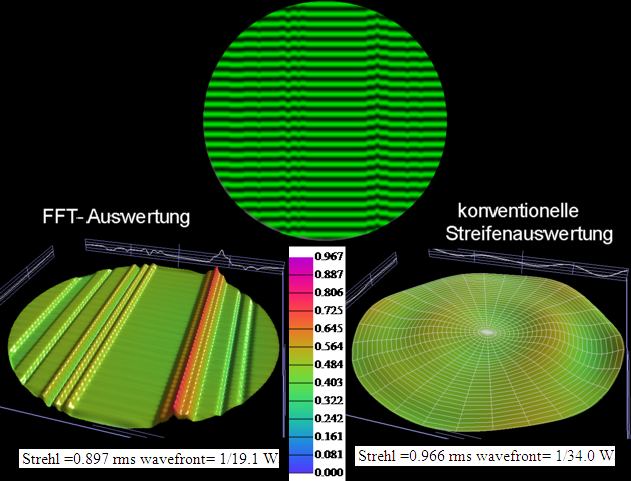
Man kommt auch mit Amateurmitteln der wahren Strehlzahl und MTF näher wenn man möglichst saubere I-Gramme mit relativ hoher Streifenzahl und dafür geeigneter Auswertesoftware wie z.B. FFT- Modus unter openFringe auswertet. Dieser Modus erlaubt es auch prüfen ob Rauheit im nennenswerten, zahlenmäßig fassbaren Ausmaß überhaupt vorhanden ist. Letzteres sei hier mit der als „A-B“ bezeichneten Methode demonstriert.
<b><b>Bild 16</b></b>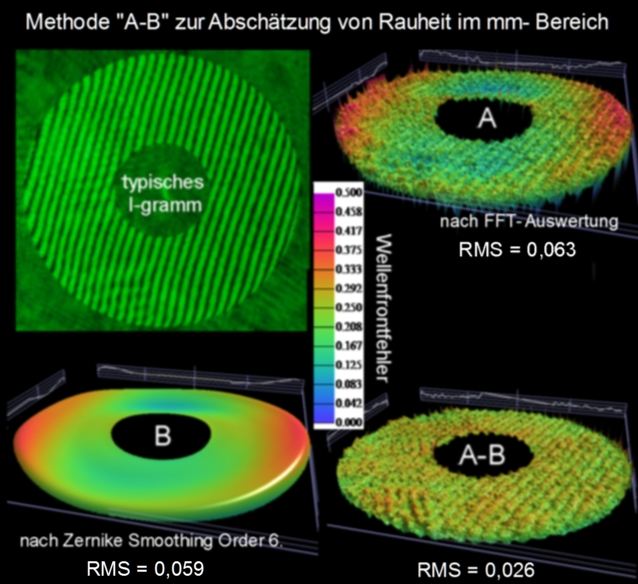
Man wertet ein relativ dichtes Streifeninterferogramm im FFT-Modus aus und erhält damit das ungefilterte Wellenfrontbild A. Selbiges wird nach <i><b>Zernike Smothing Order 6.</b></i> ausgewertet und man erhält B. <i><b>…Order 6</b></i> liefert mit B bei sehr guter Näherung ein Wellenfrontbild, welches der üblichen Streifenauswertung mit weniger Streifen entsprechen würde. Nach programmtechnischem Abzug erhält man das Wellenfrontbild A-B. Dieses ist durch Artefakte + der potenziellen Rauheit geprägt. Der Wert RMS = 0,026 ist aber bereits sehr gering. Der Anteil von Makrorauheit kann daher nur geringer sein.
Die Artefakte kann man durch Messwiederholungen, mit jeweils geänderter Streifenlage geringfügig geänderter Ausrichtung des Interferometers sowie Mittelung der A-B Einzelergebnisse unterdrücken. Das sieht dann so aus.
<b>Bild 17</b>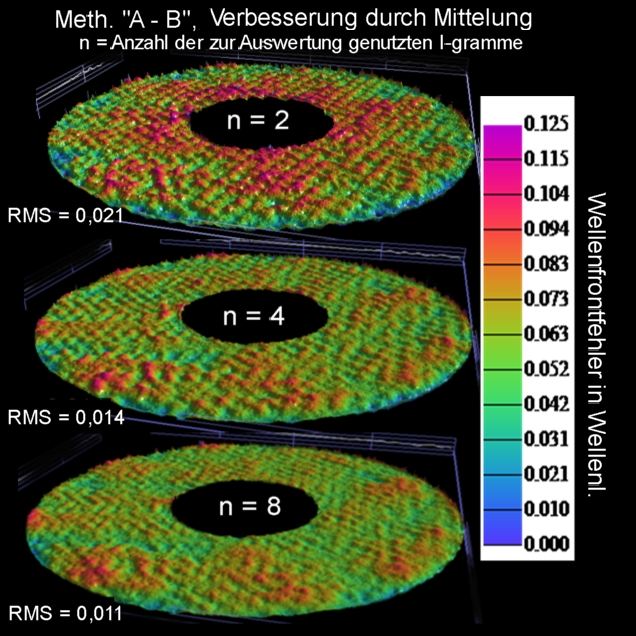
Bei Verarbeitung von n= 4 I-grammen hat man für alle nicht Zernike- Restfehle zusammen nur noch RMS = 0,014. Schlimmstenfalls wäre das eine gut reproduzierbare Maßzahl für die Rauheit. Wenn man diesen RMS in Strehl S umrechnet dann ergibt das
S = 0,992.
Wenn man dem Messaufwand nochmals verdoppelt rutscht man sogar auf RMS = 0,011, entsprechend
S = 0,995.
Anders formuliert: Die hier erfasste Makrorauheit würde schlimmstenfalls 0,5 % des Lichtes aus dem zentralen Beugungsscheibchen verdrängen. Ungefähr im gleichen Verhältnis würde die MTF gemindert. Man darf also hier mit gutem Gewissen annehmen dass die weiter oben ermittelte Strehlzahl
S = 0,96 durch Einbeziehung der Makrorauheit nicht merklich verändert wird. Man kann also darauf wetten dass bei einer Nachmessung mit einem professionellen, hoch auflösenden Interferometer die Strehlzahl ebenfalls im Bereich S = 0,95 bis 0,97 liegen wird.
<b>4.3.6.2 Mikrorauheit </b>
Nach obigem Verfahren kann submikroskopische Rauheit nicht erfasst werden. Deren RMS -Wert müsste aber ähnlich hoch sein um als potentiell störend erkannt werden zu können. Es gibt aber Hinweise aus denen man den RMS- Wert des Prüflings abschätzen kann. Danach erreicht man für besonders hochwertige Optik RMS- O(berfläche) von 0.5 nm (Quelle leider vergessen). Nach Angabe eines versierten Profis liegt der RMS-(O) bei Amateurpolitur im Bereich < 2,5 nm. Nehmen wir mal an bei unserem professionell gefertigten Prüfling beträgt diese
Gesamt- RMS(O) = 2 nm,entsprechend 4 nm Wellenfront.
Dann käme für grün = 550 nm nach der „handelsüblichen“ Strehlformel heraus:
S = e^-(2 x pi x 4/550)² = 0,998.
Nach Schroeder, „Astronomical Optics“ Kap.11 entspricht das auch dem Minderungsfaktor für die MTF (Er benutzt in seinen Formeln nur andere Symbole). Einfach gesagt der Kontrastverlust durch Mikrorauheit beträgt näherungsweise 0.2%, zu gut deutsch: forget it!
Fortsetzung mit Messung der Farbfehler und Tests im Freien folgt.
Gruß Kurt