Optisch raue Flächen sind soo böse, dass man sich da gar kein Bückelchen oder sonstwie verborgenes leisten kann, so glauben vielleicht viele. Wenn man die „mittlere“ Rauhigkeit kennt , kann man sehr simpel mit einem Taschenrechner ausrechnen wie „böse“ Rauhigkeit tatsächlich ist. Angenommen eine sonst fehlerfreie Oberfläche habe eine mittlere Rauhigkeit von PMS =1/10 lambda Wellenlänge, dann zieht das den Strehl herunter ungefähr ziemlich genau:
Strehl = e -(exp 2*pi*0,1)² = 0,67.
<b>Nachtrag 30. 08 04:</b>
Hin und wieder sieht man sich genötigt Ergänzungen nachzutragen. Man könnte sonst hier den Eindruck gewinnen ich hätte die Physik und Mathematik zur Rauhigkeit erfunden. Ich halte mich dabei lieber an Physiker und Mathematiker wie Suiter, Born, Wolf und Mahajan. Bei Suiter „Star Testing Astronomical Telescope“ findet man zur Rauhigkeit u. a. folgendes im Kapitel:
„<i>13.1 Roughness Scales and Effects
The Strehl ratio of roughness can be calculated from an approximation (Born and Wolf 1908, p. 464). Here i (index s) represents the Strehl ratio at best focus and sigmaRMS is the root mean square deviation of the Wavefront (in wavelengths) as measured from the reference sphere centered on the best focus.:
i (index s) = (näherungsweise) 1- (2* pi * sigmaRMS)². (13.1)
….Another approximation to the Strehl ratio has been given by Mahajan (1982):
i (index s) = (näherungsweise) e^(2p* sigma *RMS)² (13.2)
It gives a more accurate number than Eq at large aberration amplitudes….”</i>(Zitat Ende)
Übersetzt heißt das:
"13.1 Rauhigkeit Größenbereiche und Wirkung
Der Strehlwert der Rauhigkeit kann näherungsweise berechnet werden (Born und Wolf 1908 S. 464). Hier bedeutet is der Strehlwert bei bester Fokussierung und sigmaRMS die gemessene RMS – Abweichung der Wellenfront gemessen an der er Referenzsphäre zentriert in bester Fokussierung.
.....(13.1)
..... Formel (13.2) ergibt genauere Zahlenwerte bei größeren Amplituden der Wellenfrontabweichung...“
Mit "mitterer" Rauhigkeit meine ich die im Zitat genannten sigmaRMS.
Strehl = e -(exp 2*pi*0,1)² ist nur eine andere Schreibweise der Formel 13.2. mit 0,1 lambda Wellenfront RMS als Zahlenbeispiel.
<b>Ende Nachtrag</b>
Für solche Rauhigkeiten muss man sich aber schon gewaltig anstrengen. Mit Pechpolitur und sanftem Händchen schafft man das kaum. Das soll heißen, amateurpolierte Flächen sind meistens viel glatter. Wie glatt in RMS ausgedrückt? Das weiß ich auch nicht. Es muss auch gar nicht interessieren, wenn man denn die optische Wirkung der Rauhigkeit messen und dabei zuverlässig feststellen könnte, dass nichts messbar wichtiges verloren geht.
Dazu hab ich mir etwas ausgedacht:
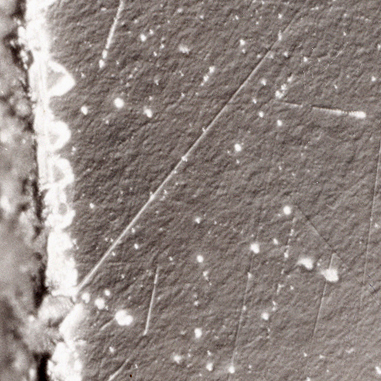
Schauen wir mal auf das erste Foto:
Bild 1
Das sind hoch vergrößerte Beugungsbilder eines künstlichen Sternes aufgenommen mit meinem 10“ f/6 Parabolspiegel bei Prüfung aus dem Krümmungsmittelpunkt gemäß folgendem Versuchsaufbau.
Bild 2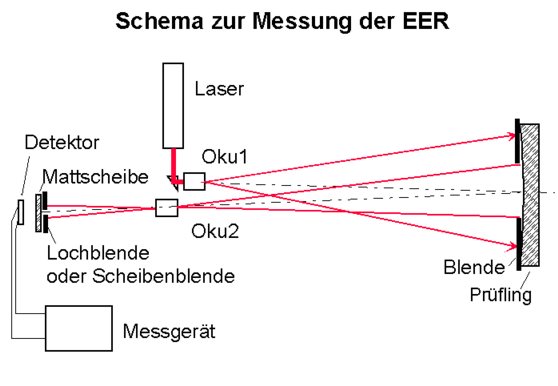
Bild 3
Die Kamera steht dort, wo der Pfeil „zum Detektor“ steht. Der Abstand vom „Oku 2“ beträgt ca. 50 cm. Das „Oku 1“ weitet den Laserstrahl auf. Der Prüfling „sieht“ daher einen künstlichen Stern. Damit dieser nicht durch die Parabolisierung des Prüflings beeinflusst wird, ist der Prüfling hier auf 118 mm Durchmesser abgeblendet. Dadurch werden auch evtl. vorhandene Zonenfehler minimiert. (Diese sollte man mit Hilfe der herkömmlichen Prüfmethoden und Korrekturtechniken schon bis zur Unkenntlichkeit beseitigt haben, was mittels Dall Null test hervorragend funktioniert). Der hier prinzipiell noch vorhandene Abweichung Parabel- Sphäre kann man gut berechnen. Sie beträgt :
P-S = r^4/R³/16/0,00055 lambda Wellenlänge
r = 118/2 mm, R= 3050 mm, lambda = 0,00055 mm
Damit wird P-S = 0,0485 lambda, also weniger als 1/20 Wellenfrontfehler als sphärische Aberration, oder theoretisch Strehl = 99,2%, wenn die Oberfläche keine nennenswerte Rauhigkeit hat. Rauhigkeit verdrängt ja wie jeder andere Fehler Lichtintensität aus dem zentralen Beugungsscheibchen und mindert somit letztendlich die Kontrastübertragung der Optik.
Wie sich das bildlich am Beugungsscheibchen zu erkennen gibt zeigen die nächsten beiden Fotos. Im ersten Falle wurde irgendeine Glasseibe vor den Prüfling gestellt, im zweiten Falle eine unbelegte Solarfolie. Wie man sieht, die vorher fast perfekten Beugungbilder (ich hab mir selber danach auf die Schulter geklopft) sind total vermatscht.
Bild 4
Bild 5
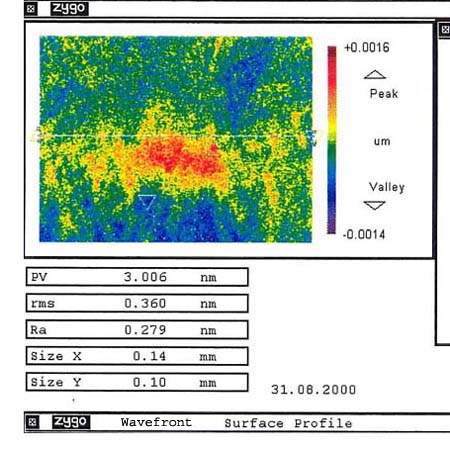
Nur wie rau diese beiden Störobjekte sind und wie schlimm der Grad ihrer Störung weiß ich immer noch nicht. Die Glasplatte hat mir bei diesem Versuch gratis ein Interferogramm an die Wand geworfen, das hier abgebildet ist.
Bild 6
Jetzt kommt der eigentliche Trick. Um den verständlich zu machen zu verstehen muss ich auf das nächste Diagramm eingehen, dass man sich mit „Aberrator“ erstellen kann.
Bild 7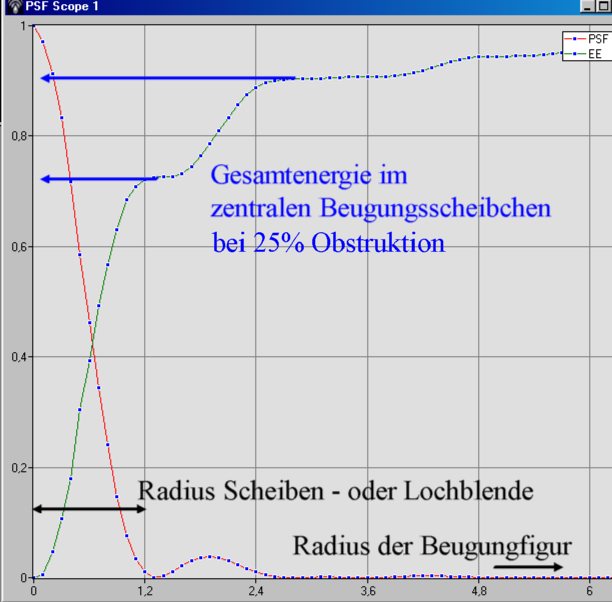
Die rote Kurve nennt man neudeutsch: PSF ( Point Spread Funktion), deutsch: Punktverteilungsfunktion. Sie zeigt nicht anderes als die normierte Intensitätsverteilung des Lichtes einer fehlerfreien Optik z. B. wie in den obigen Fotos ohne die Störungen durch Schlieren der Glasplatte bzw. in der Folie. „Normiert“ das heißt man setzt den Wert im Maximum, d.h. in der Mitte des zentralen Beugungsscheibchens = 1, auch dann, wenn die Optik Obstruktion hat. Die blaue EE- Kurve (von Encircled Energy = eingeschlossene Energie) hat es mir angetan. Sie zeigt z. B. an, welcher Anteil der gesamten durchgelassenen Lichternergie im zentralen Beugungsscheibchen (= Airy disk) gesammelt wird. Der Durchmesser DA des Airy- Disk ist für „unendlich“ weit entfernte Bildpunkte exaktgenau berechenbar nach der simplen Formel:
DA= 2,44*lambda*f/D.
Dabei ist D der Eintrittsdurchmesser der Optik und f die Brennweite. Wird wie in m obigen Versuchaufbau im Krümmungsmittelpunkt abgebildet so setzt man statt f den Krümmungsradius R in die Formel ein. Mit D 118 mm und R= 3050 mm und der Wellenlänge des Lasers von 628 nm wird der Durchmesser des Airy- Disk im Krümmungsmittelpunkt :
AD = 0,0396 mm
Das ist etwas zu winzig, um davon so schöne Beugungsbilder zu fotografieren wie oben. Also hab ich diese mit dem Oku2 (12,5 mm orth.) nach altgekannter allerdings kräftigster Okularprojektion um ca. 40 vergrößert und direkt auf den Chip der Nikon D70 projiziert.
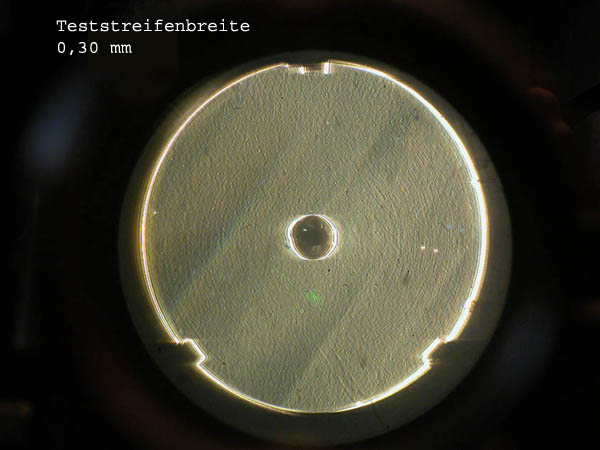
Wie ich selbiges so tat und machte, kam mir die Erleuchtung, dass man ja das Beugungsbild auch noch stärker vergrößern kann. Dank Laser ist es ja selbst bei unbelegtem Prüfling wie hier so hell, dass man es bei eingeschalteter Raumbeleuchtung auf eine Messvorrichtung projizieren kann. Die Messvorrichtung (Detektor) besteht aus einer ganz primitiven Fotozelle mit einigen cm² Fläche und einem Digitalmultimeter. Der Detektor sitzt hinter einer Mattscheibe. Auf diese Mattscheibe wird das Beugungsbild , das ist das Airy- Scheibschen mitsamt der Ringen drum herum scharf eingestellt (wie viele Ringe drum herum zu sehen sind zeigt das nächste stark überbelichtete Foto. Selbstverständlich muss man bei visuellen der Betrachtung mit dem Okular unbedingt ein Sonnenschutzfilter mindestens ND 2 einsetzen. )
Bild 8
OK, ich wollte aber messen! Das geht so:
1. Man nehme den Messwert der Fotozelle hinter der Mattscheibe.
2. Man nehme eine Lochblende die genau den Durchmesser des Airy- Disk auf der Mattscheibe hat und zentriere auf das Loch. Dann geht nur der Energieanteil des Airy- disk zum Detektor.
Wie das praktisch aussieht zeigen die nächsten Fotos.
Bild 9
Bild 10
Natürlich muss man bei der eigentlichen Messung die Raumbeleuchtung ausschalten. Dann sieht man aber keine Messwertanzeige und haut öfters mit den Pfoten unbeabsichtigt in die nicht ganz beschussfeste Messvorrichtung. Das nervt! Problemlösung: Man schalte hinter die Mattscheibe ein Gelbfilter. Das lässt das rote Laserlicht fast ungehindert durch aber kein grünes und blaues! Wie das Foto zeigt, kann man mit einer grünen LED den Messplatz genügend gut beleuchten.
Bild 11
Bei Unterbrechung des Laserstrahls zwischen Oku2 und Detektor ist die Messwertanzeige tatsächlich = 0
Weiterhin ist es mit Hilfe der Scheibenblende (Durchmesser = Lochblende) möglich . allein die Energie ohne den Betrag des Airy- Disk zu messen. Also nur die Energie die in den Beugungringen (oder was davon bei Gammel Optik übrig bleibt) zu messen. Das funktioniert ebenso gut.
Bild 12
3. Nun sind wir schon bei der Auswertung: Man teile den Messwert aus 2. durch den Messwert aus 1. Das ergibt theoretisch genau die sog EER (Encircled Energy Ratio) im Airy Disk. Diese ist bei fehlerfreier Optik genau definiert und beträgt ohne Obstruktion genau 83,96% der Gesamtintensität. Bei 33% Obstruktion sind es noch 65,33%.
Wenn ich ganz genau wüsste, dass meine Messvorrichtung die Gesamt- bzw. Teilenergie richtig anzeigt, hätte ich schon gewonnen. Jede Abweichung von den o. a. Idealwerten würde quantitativ die Wirkung von Oberflächenfehlern anzeigen. Als Messtechniker sicht man für solche Fälle nach unveränderbaren Standards, die zudem noch möglicht fehlerfrei sind. Dazu hab ich :
a) einen sphärischen Spiegel aus Quarzglas (Prüfglas für meine Cassegrain FS, daher unbelegt.)
Nach Lehrmeinung von Feinoptikern lassen sich Quarzgläser besonders glatt polieren. Damit wäre das Ding ein geeignetes „Bezugsnormal“. Dieser mit Standard A bezeichnete Prüfling ergab eine EER von 86,5%. Das wäre also ein systematischer Fehler zum Idealwert von genau 2,54%. Zur Absicherung der Empfindlichkeit hab ich diesem Prüfling genau definierte Obstruktionen verpasst. Die Ergebnisse und die berechnete Vergleichskurve zeigt das Diagramm.
Bild 13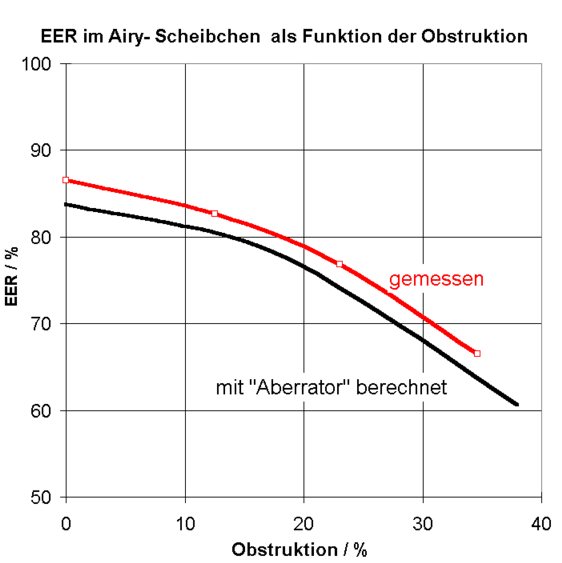
b) Mein Standard B ist eine bei Zeiss geschliffene Bikonvex- Linse mit 200 mm Brennweite und 66 mm Durchmesser. (Falls die für unsere Anwendungen rau sein sollte hör ich auf zu messen). Diese wurde auf 8,2 mm abgeblendet und der Laser in Front ca. 1,5 m entfernt aufgestellt. Damit hat der Strahlenkegel hinter der Linse recht genau die Öffnung wie bei der Messung des Standards A und anderer Prüflinge. Das Messergebnis für Standard B:
EER =86,1%
Hierbei sind höchstwahrscheinlich gegenüber Standard systematische Fehler möglich weil die Anordnung der Laserbeleuchtung geändert wurde. Bei der Nutzung von Standard A als Vergleichnormal muss nur der Prüfling in Position gebracht und kollimiert werden.
Zum Schluss noch einige weiter Messergebnisse:
Standard A mit Glasplatte im Doppelpass EER = 48,5%
Standard A mit Folie im Doppelpass EER = 66,7%
Parabolspiegel 10“ f/6 unbelegt EER = 86,4%
Parabolspiegel 8“ f/5 belegt, zwei Jahre nicht gewaschen: EER = 84,1%
dito, frisch gewaschen EER = 85,4%
Vorläufiges Fazit:
Nach den ersten Messreihen zur Reproduzierbarkeit ist eine Auflösung von besser als 1% EER bei Mittelung von 4 bis 5 Einzelwerten sehr wahrscheinlich. Weitere Versuche sind geplant.Das Schöne an der EER im Airy Disk ist noch: Bei obstruktionsfreier Optik ist der Wert praktisch gleich groß wie der Strehl- Wert.
Gruß Kurt