Hallo,
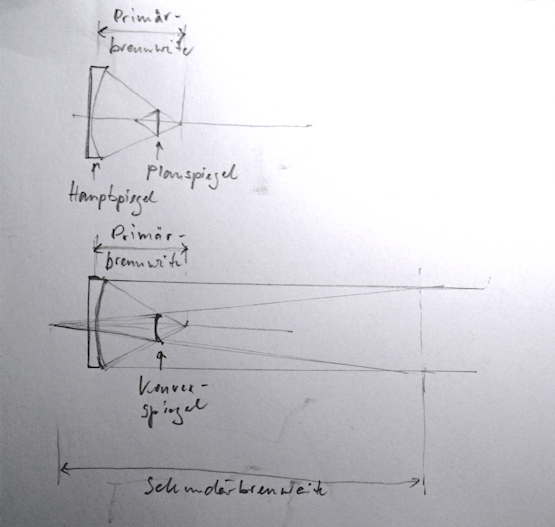
mich würde interessieren wie sich der Lichtweg (Brennweite) im Maksutov zusammensetzt.
Wenn ich bei meinem Newton den Meterstab außen ansetze, kann ich die Brennweite vom Hauptspiegel zum Fangspiegel und von da aus zum OAZ schön nachmessen.
Mein kleiner Mak (127/1500) hat ca. 31 cm Baulänge. Summiere ich die Lichtwege von der vorderen Linse zum HS, den Weg vom HS zum aufgedampften FS und den Weg vom FS zum OAZ hinaus, komme ich niemals auf 1500 mm Brennweite. Wo liegt hier mein Denkfehler?
Schöne Grüße
Rainer